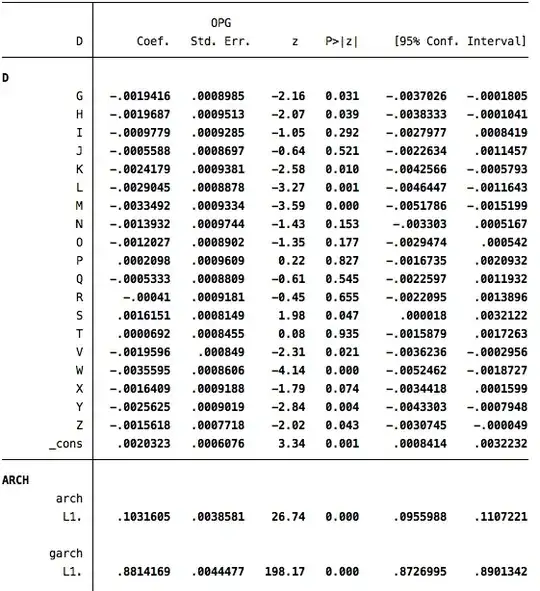
First of all, in both cases arch L1. + garch L1. is actually below 1 (although very close to 1). Or am I reading the table incorrectly?
Second, if arch L1. + garch L1. were above one (hypothetically), that would mean the variance is increasing over time, and the increase is exponential (explosive). This is undesirable.
Third, I would keep the constant in the model. The argumentation is analogous to keeping a constant in the conditional mean model: you care what moves the dependent variable away from its normal level (its mean) rather than from an arbitrary level of zero. It is similar with variance. You care about how the shocks move the conditional variance above the baseline, not above zero (zero variance is not a natural baseline, to put it loosely).
Third, the intercept of a GARCH model should be kept in the model for the following reasons.
- If you force the intercept to be zero AND the sum of ARCH and GARCH coefficients is less than one (which will happen by the design of the estimation procedure that restricts the parameters to a stationary region defined by their sum being less than one), then your model implies the conditional variance is decreasing over time, which is generally undesirable.
- If you force the intercept to be zero AND the sum of ARCH and GARCH coefficients equals one, then you end up with an EWMA estimator of the conditional variance, and the conditional variance is a random walk (which again might be undesirable).
- Also, note that testing for $\text{H}_0\colon \text{intercept}=0$ is testing a hypothesis that the parameter is on the boundary of the space (intercept cannot be negative). This might have implications on the null distribution of the test statistic, making the regular $p$-value associated with the $t$-statistic inappropriate. There might be some relevant information in Francq & Zakoian "Testing the nullity of GARCH coefficients: correction of the standard tests and relative efficiency comparisons" (2009), but I am not entirely sure.
Fourth, significance of variables is not a very strong statistical argument for choosing one model over the other. Although your boss might be more impressed if you show her a model with significant regressors, that does not mean the model would reflect the reality better. If models were chosen by significance of variables, spurious results would be widespread. (Oh, but this is actually what is happening in reality!). Instead of looking at significance of variables, look at model residuals. Check whether they match the model assumptions and are well behaved. use information criteria or cross validation for model selection. (E.g. if your goal is forecasting, pick a model with the lowest AIC or the lowest test error in leave-one-out cross validation; but note that in time series, cross validation is more complicated than in the cross sectional setting, and information criteria are the considerably easier option to use.)