14

I know that a sum of Gaussians is Gaussian. So, how is a mixture of Gaussians different?

I mean, a mixture of Gaussians is just a sum of Gaussians (where each Gaussian is multiplied by the respective mixing coefficient) right?

njk
  • 328
  • 2
  • 7

3 Answers3

7

A weighted sum of Gaussian random variables $X_1,\ldots,X_p$ $$\sum_{i=1}^p \beta_i X_i$$ is a Gaussian random variable: if $$(X_1,\ldots,X_p)\sim\text{N}_p(\mu,\Sigma)$$then $$\beta^\text{T}(X_1,\ldots,X_p)\sim\text{N}_1(\beta^\text{T}\mu,\beta^\text{T}\Sigma\beta)$$

A mixture of Gaussian densities has a density given as a weighted sum of Gaussian densities:$$f(\cdot;\theta)=\sum_{i=1}^p \omega_i \varphi(\cdot;\mu_i,\sigma_i)$$which is almost invariably not equal to a Gaussian density. See e.g. the blue estimated mixture density below (where the yellow band is a measure of variability of the estimated mixture): enter image description here

[Source: Marin and Robert, Bayesian Core, 2007]

A random variable with this density, $X\sim f(\cdot;\theta)$ can be represented as $$X=\sum_{i=1}^p \mathbb{I}(Z=i) X_i = X_{Z}$$ where $X_i\sim\text{N}_p(\mu_i,\sigma_i)$ and $Z$ is Multinomial with $\mathbb{P}(Z=i)=\omega_i$:$$Z\sim\text{M}(1;\omega_1,\ldots,\omega_p)$$

Xi'an
  • 90,397
  • 9
  • 157
  • 575
3

And here is some R code to complement @Xi'an answer:

par(mfrow=c(2,1))
nsamples <- 100000

# Sum of two Gaussians
x1 <- rnorm(nsamples, mean=-10, sd=1)
x2 <- rnorm(nsamples, mean=10, sd=1)
hist(x1+x2, breaks=100)

# Mixture of two Gaussians
z <- runif(nsamples)<0.5 # assume mixture coefficients are (0.5,0.5)
x1_x2 <- rnorm(nsamples,mean=ifelse(z,-10,10),sd=1)
hist(x1_x2,breaks=100)

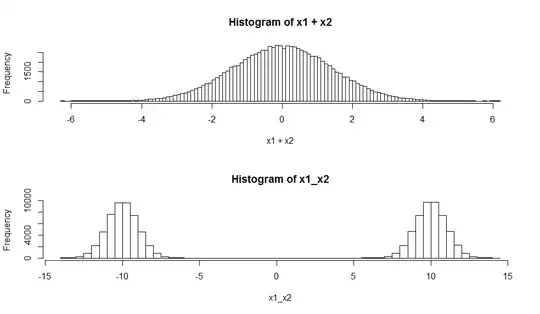
enter image description here

alberto
  • 2,646
  • 16
  • 36
1

The distribution of the sum of independent random variables is the convolution their distributions. As you have noted, the convolution of two Gaussians happens to be Gaussian.

The distribution of a mixture model performs a weighted average of the RV's distributions. Samples from (finite) mixture models can be produced by flipping a coin (or rolling a die) to decide which distribution to draw from: Say I have two RVs $X,Y$ and I want to produce an RV $Z$ whose distribution is the average of $X$ and $Y$ If I flip a coin, let $Z=X$. if I land tails, let $Z=Y$.

Christian Chapman
  • 636
  • 4
  • 13
  • Thanks enthdegree. I know that the following example is inherently wrong, but it might be interesting anyway: let's say that we have a special kind of "mixture" (if we can still call it a "mixture") of 2 Gaussian densities, where the mixing coefficients are both corresponding to 1, would that be the same of a sum of Gaussian RVs? – njk Jan 27 '16 at 11:02
  • No, although your mixture rv will be gaussian in this case, if you were to add two RVs with the component's distribution, the sum RV would have more variance than the mixture RV. – Christian Chapman Jan 27 '16 at 20:34
  • @enthdegree How is the mixture rv gaussian? It could still be bimodal if the means don't coincide, right? – learning Oct 20 '17 at 08:56
  • @learning, Yes you're right. When I wrote the prev. comment for some reason I assumed they had the same mean. – Christian Chapman Oct 21 '17 at 00:12