2

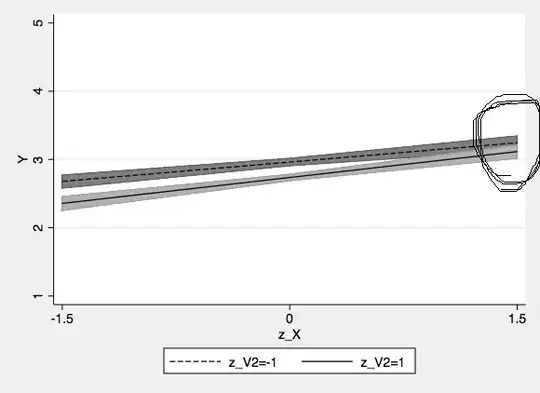
I'm exploring a significant two-way interaction in a multi-level random-effects regression. The graph (below) appears to show the interaction is driven by differences at low X, and that at high X the moderator (V2) doesn't matter. Is there a reason why I get highly significant contrasts at high X when the confidence intervals appear to overlap?

Interaction graph (circles show where the reported contrast is being conducted): fitted model regression lines

Contrast code in Stata: http://www.statalist.org/forums/forum/general-stata-discussion/general/1211045-simple-effects-after-regression

Contrast test at high X (circled on the graph):

      Y   |      Coef.   Std. Err.      z    P>|z|     [95% Conf. Interval]
----------+-------------------------------------------------------------------
z_X = 1.5 |  -.1288761   .0471769    -2.73   0.006    -.2213412   -.0364111
------------------------------------------------------------------------------

That's surprising. Is this something to do with multi-level (nested/panel) data? I'm not very familiar with inferential stats using multiple levels simultaneously. I would have expected that if the 95% confidence intervals overlap, as they clearly do for z_X = 1.5, that the contrast there would be not significant or close to that. Thanks for reading.

The following are relevant posts, but I sadly admit I did not follow the explanations: Relation between confidence interval and testing statistical hypothesis for t-test

Large overlap between confidence intervals, although z test for difference was significant

I'm also new around here, so please let me know if I could improve how I asked this question.

Community
  • 1
Cameron Brick
  • 121
  • 3
  • I've added the image to the body of the question for you (which you'll be able to do once you've got sufficient reputation) – James Stanley Apr 16 '15 at 22:53
  • You say "I would have expected that if the 95% confidence intervals overlap, as they clearly do for z_X = 1.5..." -- are you basing this on the confidence bands overlapping in the graph, or on some other information? – James Stanley Apr 16 '15 at 22:54
  • The existence of overlap at some given (high) x-value isn't really related to whether there's a significant *interaction*. Indeed, its not clear to me why the picture should lead to any surprise -- it's entirely consistent with a significant interaction. You could also see overlap near the ends of the range when there was just a significant main effect. – Glen_b Apr 16 '15 at 23:52
  • Overlapping CIs of two estimates does not necessarily mean the difference of the estimates is not significant. This is just another example where that happened to be the case. – Affine Apr 21 '15 at 21:08
  • The explanation for the univariate t-test should give you an idea of why that is. http://www.cscu.cornell.edu/news/statnews/Stnews73insert.pdf ; [image mirror](http://i.stack.imgur.com/HIbZK.png) – Affine Apr 21 '15 at 21:11
  • I'm sorry, I appear to have been a bit unclear. The interaction is significant, small effect size standardized b = .03. Then I tested for what I call above "contrasts," that is, tests of equivalence for values of Y at high vs. low V2 at low X, highly significant; then values of Y at high vs. low V2 at high X, and that's the stat I quoted initially, and based on visual inspection of the graph's CIs I didn't think it would be significant but it was. I don't think the question has been answered yet. Thanks James for image posting! – Cameron Brick Apr 21 '15 at 20:59
  • That is a great explanation. – Cameron Brick Apr 21 '15 at 21:39

2 Answers2

1

The fact that the confidence intervals overlap does not mean that the difference is not significant, and this is true for all statistical models, including simple linear regression.

"Confidence intervals not overlapping" is substantial more conservative than the equivalent p value.

Peter Flom
  • 94,055
  • 35
  • 143
  • 276
0

Interaction effects imply that your x variable on the graph has different effects depending on which of the two binary levels the subject falls into.

You are reading the graph correctly, and it implies that the binary variable has no effect at high values of x. However the fact that the two groups behave differently for low and high values of x is itself the definition of an interaction effect.

analystic
  • 725
  • 1
  • 5
  • 21