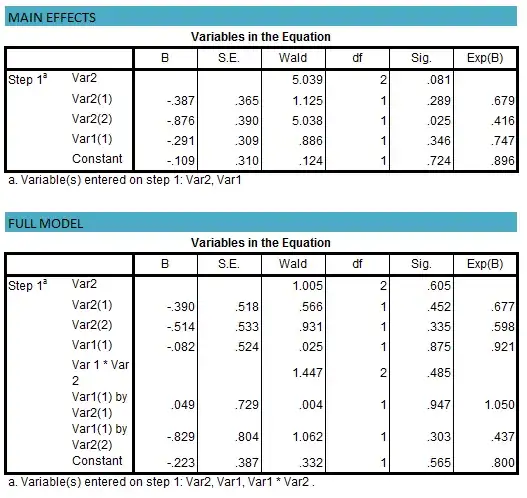
The interpretation of your coefficient for Var2(2) in the presence of an interaction is that, that is the effect on the DV when all variables it interacts with are 0. So what you are looking at is not a main effect, but the simple effect of Var2(2) when the person is in the control condition of Var1. To get the main effects, you need to contrast code your predictors (sum to zero codes, rather than dummy codes). In SPSS Helmert coding and polynomial coding are both sum to zero codes. There may be others, but I don't have SPSS in front of me to check.
Additionally, these individual effects (Var2(1) and Var2(2)) are not main effects. They are contrast effects or simple main effects (different nomenclature, same thing). For categorical variables with more than 2 levels, the main effect is the joint effect of all contrasts (for Var2 the joint effect of both Var2(1) and Var2(2)). If you really want the main effect (you may truly only be interested in the contrasts) you need to compare your model
$$y=\beta_0+\beta_1*VAR1_1+\beta_2*VAR2_1+\beta_3*VAR2_2+\beta_4*VAR1_1*VAR2_1+\beta_5*VAR1_1*VAR2_2+\epsilon$$
against a model that removes both VAR2 variables (but leaves the interactions):
$$y=\beta_0+\beta_1*VAR1_1+\beta_4*VAR1_1*VAR2_1+\beta_5*VAR1_1*VAR2_2+\epsilon$$
The easiest way to do this is to not use categorical variables. You will need to create new numeric variables based on the categorical variables. For VAR1 the value should be -1 if control and 1 if not control. For VAR2 you will need two variables. The contrast depends on what's if interest to you, but probably you'd want the following. For VAR2(1) the value would be -2 if control and 1 if either of the treatments. For VAR2(2) the value should be 0 if control and -1 for one treatment and 1 for the other. Next, you need to create the interactions. Again there are 2. Multiply VAR1 by VAR2(1) to create one interaction, and VAR1 by VAR2(2) for the second interaction. As an aside, these are the same as the sum-to-zero contrasts I mentioned. Specifically, these are Helmert contrasts.
Then go back to the logistic regression dialogue box and use all of those variables as continuous predictors. Get your model. Then do another logistic regression that only has VAR1, Interaction1 and Interaction2. Get your model. Both results should tell what the deviance is for the model. Subtract the deviance from the first model from deviance from the second model. This a Chi-squared value. You can do a Chi-squared test with one degree of freedom and that value as your test statistic (here's an online calculator for it).
As you can see its a little complicated. There may be an easier way in SPSS. I'm not a regular user. Again, though, you may not be interested in the main effect. The main effect just tells you that VAR2 accounts for significant variance in the model. However, it doesn't tell you anything about the effect of VAR2 (does it increase your DV or decrease it). The contrasts tell you that. Since you seem to not be familiar with contrasts, I suggest you read up a bit on them. You can't interpret regression results without knowing what is going on. Here is a place to start. Here's some more. Finally, here's some reading on what a main effect is, and here's some reading on interpreting coefficients when interactions are in your model.
Also, while it is not of focal interest, your intuition about the interaction not affecting the main effect because it is not significant isn't correct. Not significantly different from 0 does not mean the interaction equals 0. Not being significant just means you don't have enough evidence to say the size of the interaction isn't 0. The interaction still picks up a chunk of variance in addition to changing how you interpret lower order coefficients.