4

So I've made a linear regression of my two variables using pythons np.polyfit.

This is my code:

    p = np.polyfit(lengths, breadths, 1)
    m = p[0]
    b = p[1]
    sumOfSquares(m,b,breadths,lengths)
    newlengths = []
    for y in lengths:
        newlengths.append(y*m+b)
    ax.plot(lengths, newlengths, '-', color="#2c3e50")

I find the sum of squares with this code:

def sumOfSquares(m,b,breadths,lengths):
    sum = 0
    for i in range(0,len(breadths)):
        sum += ((breadths[i]-(lengths[i]*m+b))**2)
    print sum
    print sum**(1/2)/(len(lengths))

The sum of squares is 7978.2877 While the average residual element is 0.00224

How do I quantify how good linear regression this really is? My goal is to prove linearity between lengths and breadths. The data, plottet against the linear regression line

bjornasm
  • 171
  • 6
  • 19
    This is the most linear linear regression I've ever seen. – Sycorax Apr 14 '15 at 17:01
  • It's not entirely clear (at least to me) what's being asked. You have the residuals - are you concerned that the residuals aren't capturing some interesting aspect of your model's fit? – Louis Cialdella Apr 14 '15 at 17:17
  • Excuse me for my unclarity @LCialdella . I'm simply asking - how would I know if I should be content with my residual? Is there any way to quantify that its OK? Should I use an other measurement than residuals to check my models fit? – bjornasm Apr 14 '15 at 17:20
  • 2
    The residuals can be used to compare models, but there's is not an obvious way I can think of to accept or reject a particular residual value (unless you want to construct a hypothesis test of some kind). However, if you are specifically trying to gauge whether or not the relationship is linear, you may want to look at calculating the [Pearson correlation](http://en.wikipedia.org/wiki/Pearson_product-moment_correlation_coefficient), which will give you a nice normalized value. – Louis Cialdella Apr 14 '15 at 17:25
  • 1
    Can it be that you are searching for something like [Regression Diagnostics](http://www.statmethods.net/stats/rdiagnostics.html) (the link is for R but there must be something similar for python)? There is also [Ramsei test](http://en.wikipedia.org/wiki/Ramsey_RESET_test), which "tests whether non-linear combinations of the fitted values help explain the response variable". – lanenok Apr 14 '15 at 18:16
  • 2
    Additionally, it may help to square the Pearson correlation to yield the [coefficient of determination](http://en.wikipedia.org/wiki/Coefficient_of_determination), or more commonly known as the R^2, which will provide you with the percentage of variance in breadths that can be explained with lengths. – Matt Reichenbach Apr 14 '15 at 18:56
  • Possible duplicate of [In what order should you do linear regression diagnostics?](https://stats.stackexchange.com/questions/32600/in-what-order-should-you-do-linear-regression-diagnostics) – kjetil b halvorsen Nov 23 '18 at 14:46
  • 1
    @Sycorax This regression is not unusual, it is quite common when the correct procedure for relating variables is followed, when the problem has balanced physical units, and when deterministic cause and effect are explored and exploited. – Carl Nov 23 '18 at 20:35
  • @Sycorax: as Carl is stating, when using linear regression to set for calibration of instruments, this plot could actually show *too weak* a linear relation between *x* and *y*. If I recall from my Chem 101 class, in many cases $\hat \rho < 0.95$ was unacceptably high error in many cases (or maybe it was 0.99?) – Cliff AB Nov 23 '18 at 21:46
  • @CliffAB As good as one can get; the more practical limits are often what percentage error (if error is proportional) or what 95% CI for results one can achieve. Usually the question occurs in the context of comparison studies, so the best test is (usually) the least incorrect one, although there can be other considerations, not all of them rational. – Carl Nov 23 '18 at 22:44
  • This is the best best comment I have ever seen – Sebastian Nov 23 '18 at 23:51
  • 1
    @Carl I think your explanation provides a strong explanation for why such strong linear effects are not commonly observed — people don’t constrain themselves to these conditions. – Sycorax Nov 24 '18 at 18:54

2 Answers2

1

Clearly, this question is asking for tests of linearity. Tests for linearity, including cumulative sum control chart CUSUM, are reviewed here. These include tests called

Frequency Domain tests by Subba Rao and Gabr, and Hinnich
Time series tests squares of time series data, the Portmanteau test and CUSUM, 
  the Test for additivity, the Score Test, the Bootstrapped COX test, 
  and the Neyman-Pearson test 
Linearity tests against specific alternatives

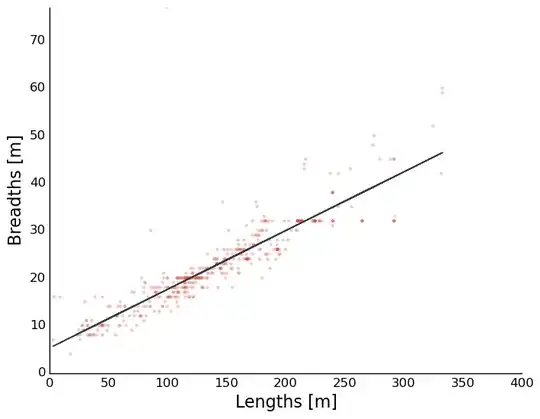
Which test should be used to test for non-linearity is itself subject to testing. The first, most common test, and one that applies to everything, is to plot residuals, i.e., the difference between the model and the data points, and examine them. If these are flat (e.g., not u-, n-, w- or m-shaped), then linearity is not ruled out. Beyond plotting, which linearity test is appropriate depends on the circumstances. For example, one problem with ordinary least squares is that sometimes the residuals may trend linearly. This is because least squares in $y$ minimizes the error in estimating $y$ and is sometimes not a best functional relationship between $x$ and $y$. Thus, a second order test of residuals is to fit those residuals with an ordinary least squares line to see if the slope is zero or not. Zero slope of residuals will occur when, for example, the $x$-values are equidistant as they would be in some time series, and there are other conditions as well that result in an absence of slope bias of residuals. If the slope is zero (to within machine precision, this is not subtle), then the conditions are met to use a CUSUM linearity test. If the slope of residuals is not zero, the problem may be bivariate, and certain measures, e.g., CUSUM or R$^2$, would be misleading. To overcome this, bivariate regression, e.g., a Deming regression or, in some circumstances a Passing-Bablok regression, can identify a best linear functional relationship without residual linear bias. In those bivariate cases, the CUSUM algorithm can be used to test for linearity.

There are lots of tests, not just CUSUM, not just adjusted-R$^2$. Regarding adjusted-R$^2$, this does not test specifically for linearity/non-linearity. For example, without testing for collinearity, and a separate linearity test of the highly collinear parameters, adjusted-R$^2$ alone would miss the source of the non-linearity. Adjusted-R$^2$ would fall under linearity tests against specific alternatives in the classification above, precisely because it does not test for non-linearity but for all sources of error including noise. To convert R$^2$ to measure non-linearity, or more precisely modeling error, the noise error would have to be modeled and removed. That was done in this paper, see the Appendix Section.

If more information is desired, please say so. Bivariate regression references below.

A New Biometrical Procedure for Testing the Equality of Measurements from Two Different Analytical Methods H. Passing, W. Bablok, J. Clin. Chem. Biochem. Vol 21 No. 11 1983; 709-720

Comparison of Several Regression Procedures for Method Comparison Studies and Determination of Sample Sizes H. Passing, W. Bablok, J. Clin. Chem. Biochem. Vol 22 No. 6 1984; 431-445

A General Regression Procedure for Method Transformation H. Passing, W. Bablok, J. Clin. Chem. Biochem. Vol 26 No. 11 1988; 783-790

Evaluation of Regression Procedures for Method Comparison Studies Kristian Linnet, Clin.Chem. Vol. 39 No. 3 1993; 424-432

Incorrect Least-Squares Regression Coefficients in Method-Comparison Analysis P. Joanne Cornbleet, Nathan Gochman, Clin Chem. Vol 25 No. 13 1979; 432-437

Estimation of the Linear Relationship Between the Measurements of Two Methods with Proportional Errors Kristian Linnet, Statistics in Medicine Vol 9 1990; 1463-1473

Performance of Deming regression analysis in case of misspecified analytical error ratio in method comparison studies Kristian Linnet,Clin Chem. Vol 44 No. 5 1998; 1024-1031

Necessary Sample Size for Method Comparison Studies Based on Regression Analysis Kristian Linnet, Clin Chem. Vol 45 No. 6 1999; 882-894

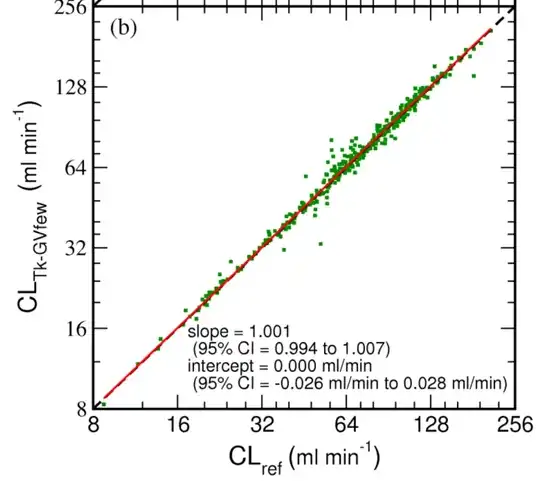
One image from a methods comparison study for @Sycorax showing that in certain contexts good agreement between methods can be achieved. There are many such contexts.

enter image description here

Finally, the plot shown in the question appears (from personal experience) to have residual non-zero slope. This is likely a bivariate problem. Test the residuals' slope before choosing a test for linearity. P.S. Residual slope testing is done nonparmaterically, i.e., using rank ordered residuals: 1,2,3,4,... not parametrically (x1,x2,x3,x4,...).

Carl
  • 11,532
  • 7
  • 45
  • 102
  • "One problem with ordinary least squares is that the residuals may trend linearly": I think you mean "...may trend *non* linearly."? – Cliff AB Nov 23 '18 at 19:31
  • @CliffAB Well both. I'll put in some more text to explain better. – Carl Nov 23 '18 at 19:39
1

"Proof" is tricky. You can show evidence. The plot itself is very strong evidence. So, I might just post the plot and say "Ecce liniabilium" (behold linearity).

If you want something a little fancier, I'd fit a restricted cubic spline to the data, then plot the results. I'd add the spline to the plot you've got (I bet they nearly coincide) and I might even compare the predicted values. If you insist on some sort of test, you could do a paired t-test of the predicted values from the two models.

Peter Flom
  • 94,055
  • 35
  • 143
  • 276