Question: problem statement
$$z^d = \sum_i x_i^d $$
pdf of $X = \frac{d(\lambda x^d)^n}{x \Gamma(n)} \exp(-\lambda x^d)$ which is a generalized Gamma distribution and they represent euclidean distances. The pdf is presented in Eq(26) http://www.cs.tut.fi/~moltchan/pubs/distances2011.pdf
I am not sure, if each of the r.v for distance is independent. I obtained a histogram of the distances calculated between data points of a univariate time series model of Moving Avreage (FIR filter) in higher dimension $d$ for the 2 cases
(a) when the time series is clean given below
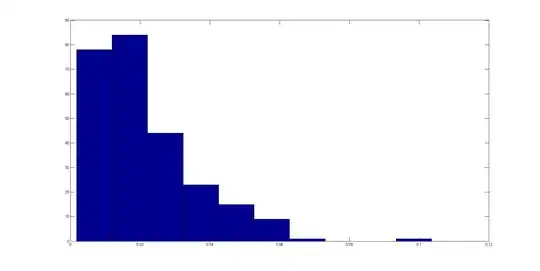
and when the time series signal is noisy with a signal to noise ratio of 1 db. The noise added is a zero mean white gaussian noise.
Question1: I do not know how to check if they are indeed Generalized gamma.