Thanks for @TommyL's answer, but his answer is not direct on the construction of $X$ and $y$. I somehow "solve" this myself. First, when $\lambda$ increases, $\|\beta^*\|_2$ will not increase when each $\beta^*_i$ decreases monotonically. This happens when $X$ is orthonormal, in which we have
$$
\beta^*_i=\mathrm{sign}(\beta_i^{\mathrm{LS}})(\beta_i^{\mathrm{LS}}-\lambda)_+
$$
Geometrically, in this situation $\beta^*$ moves perpendicularly to the contour of the $\ell_1$ norm, so $\|\beta^*\|_2$ cannot increase.
Actually, Hastie et al. mentioned in the paper Forward stagewise regression and the
monotone lasso, a necessary and sufficient condition of the monotonicity of the profile paths:

In Section 6 of the paper they constructed an artificial data set based on piecewise-linear basis functions which violates the above condition, showing the non-monotonicity. But if we have luck, we can also create a random data set demonstrating the similar behavior but in a simpler way. Here is my R code:
library(glmnet)
set.seed(0)
N <- 10
p <- 15
x1 <- rnorm(N)
X <- mat.or.vec(N, p)
X[, 1] <- x1
for (i in 2:p) {X[, i] <- x1 + rnorm(N, sd=0.2)}
beta <- rnorm(p, sd=10)
y <- X %*% beta + rnorm(N, sd=0.01)
model <- glmnet(X, y, family="gaussian", alpha=1, intercept=FALSE)
I deliberately let $X$'s columns highly correlated (far from the orthonormal case), and the true $\beta$ have both large positive and negative entries. Here is $\beta^*$'s profile (not surprisingly only 5 variables are activated):
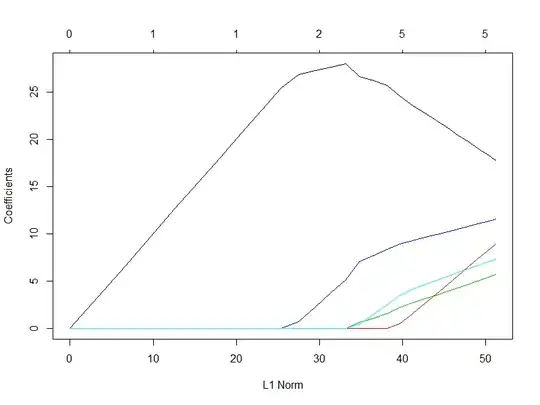
and the relation between $\lambda$ and $\|\beta^*\|_2$:
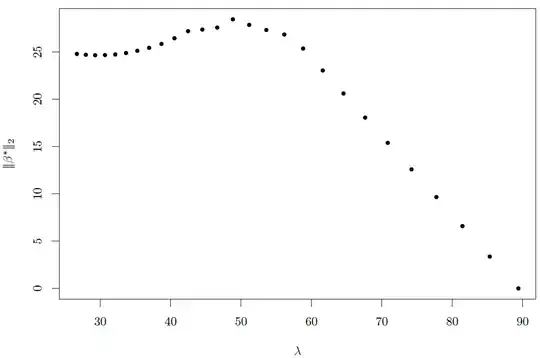
So we can see that for some interval of $\lambda$, $\|\beta^*\|_2$ increases as $\lambda$ increases.