I'm using MATLAB R2015a, glmfit function for training and glmval for out of sample evaluation. My input sample and out-of-sample are normalized (MAX-MIN mapping / Using MAX-MIN of training sample set for normalizing out-of-sample data set).
When I'm suing SVM or MLP model there isn't any problem and I have output values for all out-of-samples but when I check Logistic Regression outputs, in some samples I have NAN as output.
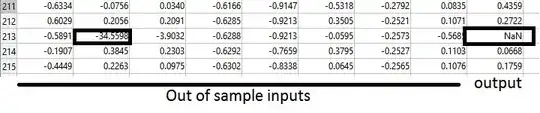
In cases that we have NAN as output, all inputs are negative (or many of them) as we can see in above picture. The above data set is out-of-sample that we used to predict output probabibites after model training phase. Why Logistic Regression returns Nan output for these samples?
PS. In training phase I have this error :
Warning: Iteration limit reached.
Model information :
log Likelihood : -1.2241758
SST = 80
SSR = 40.5388
DFE = 307
Estimated Coefficients:
Estimate SE tStat pValue
________ _______ ________ __________
(Intercept) 2.0485 0.40146 5.1027 3.3484e-07
x1 -6.5222 1.4907 -4.3751 1.2136e-05
x2 1.3972 0.3009 4.6434 3.4269e-06
x3 -8.7807 2.7749 -3.1644 0.0015542
x4 96.094 180.41 0.53265 0.59427
x5 0.042014 0.77166 0.054446 0.95658
x6 -0.75486 0.72205 -1.0454 0.29582
x7 1.1678 0.98433 1.1864 0.23548
x8 1.9328 0.73925 2.6146 0.0089338
x9 -0.65827 0.2902 -2.2683 0.02331
x10 -102.83 180.47 -0.56982 0.5688
x11 1.3374 0.62117 2.1531 0.031311
x12 -0.43609 0.61412 -0.71011 0.47764
320 observations, 307 error degrees of freedom
Dispersion: 1
Chi^2-statistic vs. constant model: 199, p-value = 5.83e-36