PDF of a sum of dependent variables

Question

This is a direct continuation of my recent question. The thing that I actually want to get is the distribution of $a+d+\sqrt{(a-d)^2+4bc}$, where $a,b,c,d$ are uniform in $[0,1]$. Now, the distribution of $(a-d)^2+4bc$ was successfully computed in the mentioned thread, and let's call it $h(x)$. The distribution of $\sqrt{(a-d)^2+4bc}$ is simply $h(x^2)\cdot 2x$. The last step would be to compute the distribution of the sum of $X=a+d$ and $Y=\sqrt{(a-d)^2+4bc}$ in a way similar to the previous one, but $X$ and $Y$ are not independent, and now I'm stuck and don't even know where to start with.

It may be useful to note that $\sqrt{(a-d)^2+4bc}=\sqrt{(a+d)^2-4(ad-bc)}$ and in the latter the components under the root (i.e., $X^2=(a+d)^2$ and $W=-4(ad-bc)$) are easy to calculate. Then, I'm interested in the distribution of $X+\sqrt{X^2+W}$, knowing the distributions of $X$ and $\sqrt{X^2+W}$.

I don't see any useful change of variables. I thought about using conditional probability, but how can I find $f(\sqrt{X^2+W}\Big|X)$? I might be too much ahead and maybe have to go back a few steps.

Is it even possible to calculate something like this?

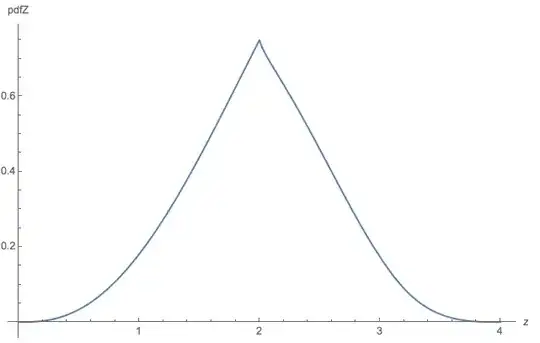
The resulting distribution should look like this:

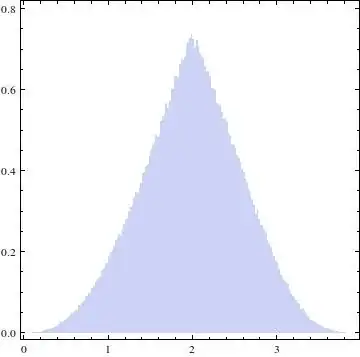
EDIT: The accepted answer gives the solution I was looking for, however, I'm still curious how to derive it analytically. I mean, in my previous question the CDF was given as an integral:

$\int_0^4 F(\delta-y)g(y)dy$

with $F$ and $g$ given by simple functions. Theoretically, that could be integrated using pen and paper. Of course using software is natural. However, I'm still curious how to give a closed-form answer here. wolfies answer rings a bell, but... A convolution of three pdfs of such a (relatively) complicated function?

Answer 1

Find the pdf of: $\quad A+D+\sqrt{(A-D)^2+4BC}, \quad $ where $A,B,C,D$ are iid $Uniform(0,1)$

Let $U = 4 BC$, where $U$ has pdf: $\quad g(u) = \frac{1}{4} \log \left(\frac{4}{u}\right) \quad \text{for } 0<u<4$.

This reduces the problem from 4 to 3 independent random variables. Then, by independence, the joint pdf of $(A,D,U)$ is $f(a,d,u)$:

Let $Z = A+D+\sqrt{(A-D)^2+4BC}$. The cdf of $Z$ is $P(Z<z)$:

where I am using the Prob function from the mathStatica package for Mathematica to automate the nitty-gritties.

The pdf of $Z$ is simply the derivative of the latter wrt $z$, which yields the solution:

All done.

Here is a plot of the exact theoretical pdf of $Z$:

Monte Carlo check

The following diagram compares an empirical Monte Carlo approximation of the pdf (squiggly blue) to the theoretical pdf derived above (red dashed). Looks fine.

Answer 2

Just after reading wolfies answer I understood I could calculate the final distribution from the very beginning without all the mid-point steps:

M[x_] := M[x] = Evaluate@FullSimplify@ Integrate[ Boole[a + d + Sqrt[(a - d)^2 + 4 b c] <= x], {a, 0, 1}, {b, 0, 1}, {c, 0, 1}, {d, 0, 1}] gives the CDF and

m[x_] := m[x] = Evaluate@FullSimplify@D[M[x], x] gives the PDF that works perfect with my simulation:

This uses directly the approach of an answer to my previous question.