I read this statement on one old true/false exam:
We can get multiple local optimum solutions if we solve a linear regression problem by minimizing the sum of squared errors using gradient descent.
Solution: False
My question is, which part of this question is wrong? Why is this statement false?
This question is interesting insofar as it exposes some connections among optimization theory, optimization methods, and statistical methods that any capable user of statistics needs to understand. Although these connections are simple and easily learned, they are subtle and often overlooked.
To summarize some ideas from the comments to other replies, I would like to point out there are at least two ways that "linear regression" can produce non-unique solutions--not just theoretically, but in practice.
The first is when the model is not identifiable. This creates a convex but not strictly convex objective function which has multiple solutions.
Consider, for instance, regressing $z$ against $x$ and $y$ (with an intercept) for the $(x,y,z)$ data $(1,-1,0),(2,-2,-1),(3,-3,-2)$. One solution is $\hat z = 1 + y$. Another is $\hat z = 1-x$. To see that there must be multiple solutions, parameterize the model with three real parameters $(\lambda,\mu,\nu)$ and an error term $\varepsilon$ in the form
$$z = 1+\mu + (\lambda + \nu - 1)x + (\lambda -\nu)y + \varepsilon.$$
The sum of squares of residuals simplifies to
$$\operatorname{SSR} = 3\mu^2 + 24 \mu\nu + 56 \nu^2.$$
(This is a limiting case of objective functions that arise in practice, such as the one discussed at Can the empirical hessian of an M-estimator be indefinite?, where you can read detailed analyses and view plots of the function.)
Because the coefficients of the squares ($3$ and $56$) are positive and the determinant $3\times 56 - (24/2)^2 = 24$ is positive, this is a positive-semidefinite quadratic form in $(\mu,\nu,\lambda)$. It is minimized when $\mu=\nu=0$, but $\lambda$ can have any value whatsoever. Since the objective function $\operatorname{SSR}$ does not depend on $\lambda$, neither does its gradient (or any other derivatives). Therefore, any gradient descent algorithm--if it does not make some arbitrary changes of direction--will set the solution's value of $\lambda$ to whatever the starting value was.
Even when gradient descent is not used, the solution can vary. In R, for instance, there are two easy, equivalent ways to specify this model: as z ~ x + y or z ~ y + x. The first yields $\hat z = 1 - x$ but the second gives $\hat z = 1 + y$.
> x <- 1:3
> y <- -x
> z <- y+1
> lm(z ~ x + y)
Coefficients:
(Intercept) x y
1 -1 NA
> lm(z ~ y + x)
Coefficients:
(Intercept) y x
1 1 NA
(The NA values should be interpreted as zeros, but with a warning that multiple solutions exist. The warning was possible because of preliminary analyses performed in R that are independent of its solution method. A gradient descent method would likely not detect the possibility of multiple solutions, although a good one would warn you of some uncertainty that it had arrived at the optimum.)
Strict convexity guarantees a unique global optimum, provided the domain of the parameters is convex. Parameter restrictions can create non-convex domains, leading to multiple global solutions.
A very simple example is afforded by the problem of estimating a "mean" $\mu$ for the data $-1, 1$ subject to the restriction $|\mu| \ge 1/2$. This models a situation that is kind of the opposite of regularization methods like Ridge Regression, the Lasso, or the Elastic Net: it is insisting that a model parameter not become too small. (Various questions have appeared on this site asking how to solve regression problems with such parameter constraints, showing that they do arise in practice.)
There are two least-squares solutions to this example, both equally good. They are found by minimizing $(1-\mu)^2 + (-1-\mu)^2$ subject to the constraint $|\mu| \ge 1/2$. The two solutions are $\mu=\pm 1/2$. More than one solution can arise because the parameter restriction makes the domain $\mu \in (-\infty, -1/2]\cup [1/2, \infty)$ nonconvex:
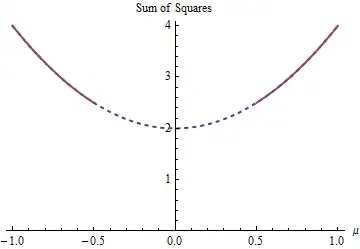
The parabola is the graph of a (strictly) convex function. The thick red part is the portion restricted to the domain of $\mu$: it has two lowest points at $\mu=\pm 1/2$, where the sum of squares is $5/2$. The rest of the parabola (shown dotted) is removed by the constraint, thereby eliminating its unique minimum from consideration.
A gradient descent method, unless it were willing to take large jumps, would likely find the "unique" solution $\mu=1/2$ when starting with a positive value and otherwise it would find the "unique" solution $\mu=-1/2$ when starting with a negative value.
The same situation can occur with larger datasets and in higher dimensions (that is, with more regression parameters to fit).
I'm afraid there is no binary answer to your question. If Linear regression is strictly convex (no constraints on coefficients, no regularizer etc.,) then gradient descent will have a unique solution and it will be global optimum. Gradient descent can and will return multiple solutions if you have a non-convex problem.
Although OP asks for a linear regression, the below example shows least square minimization although nonlinear (vs. linear regression which OP wants) can have multiple solutions and gradient descent can return different solution.
I can show empirically using a simple example that
Consider the example where you are trying to minimize least squares for the following problem:
where you are trying to solve for $w$ by minimizing objective function. The above funtion although differentiable is non-convex and can have multiple solution. Substituting actual values for $a$ see below.
$a_{12} =9,a_{13} = 1/9,a_{23}=9,a_{31}=1/9$
$minimize$ ${(9-\frac{w_1}{w_2})^2+(\frac{1}{9}-\frac{w_1}{w_3})^2+(\frac{1}{9}-\frac{w_2}{w_1})^2+(9-\frac{w_2}{w_3})^2+(9-\frac{w_3}{w_1})^2+(\frac{1}{9}-\frac{w_3}{w_2})^2}$
The above problem has 3 different solution and they are as follows:
$w = (0.670,0.242,0.080),obj = 165.2$
$w = (0.080,0.242,0.670),obj = 165.2$
$w = (0.242,0.670,0.080),obj = 165.2$
As shown above the least squares problem can be nonconvex and can have multiple solution. Then above problem can be solved using gradient descent method such as microsoft excel solver and every time we run we end up getting different solution. since gradient descent is a local optimizer and can get stuck in local solution we need to use different starting values to get true global optima. A problem like this is dependent on starting values.
This is because the objective function you are minimizing is convex, there is only one minima/maxima. Therefore, the local optimum is also a global optimum. Gradient descent will find the solution eventually.
Why this objective function is convex? This is the beauty of using the squared error for minimization. The derivation and equality to zero will show nicely why this is the case. It is pretty a textbook problem and is covered almost everywhere.
