Smoothing - when to use it and when not to?

Question

There is quite an old post on William Briggs' blog which looks at the pitfalls of smoothing data and carrying that smoothed data through to analysis. The key argument is namely:

If, in a moment of insanity, you do smooth time series data and you do use it as input to other analyses, you dramatically increase the probability of fooling yourself! This is because smoothing induces spurious signals—signals that look real to other analytical methods. No matter what you will be too certain of your final results!

However, I am struggling to find comprehensive discussions as to when to smooth and when not to.

Is it only frowned upon to smooth when using that smoothed data as an input to other analysis or are there other situations when smoothing is not advised? Conversely, are there situations where smoothing is advised?

Answer 1

Exponential Smoothing is a classic technique used in noncausal time series forecasting. As long as you only use it in straightforward forecasting and don't use in-sample smoothed fits as an input to another data mining or statistical algorithm, Briggs' critique does not apply. (Accordingly, I am skeptical about using it "to produce smoothed data for presentation", as Wikipedia says - this may well be misleading, by hiding the smoothed-away variability.)

Here is a textbook introduction to Exponential Smoothing.

And here is a (10-year-old, but still relevant) review article.

---

EDIT: there seems to be some doubt about the validity of Briggs' critique, possibly somewhat influenced by its packaging. I fully agree that Briggs' tone can be abrasive. However, I'd like to illustrate why I think he has a point.

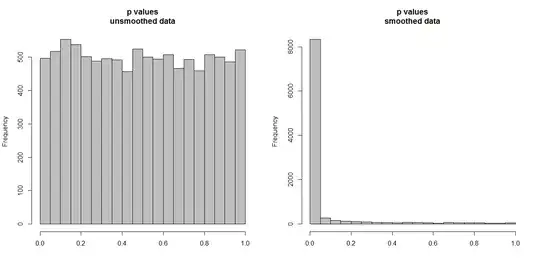
Below, I'm simulating 10,000 pairs of time series, of 100 observations each. All series are white noise, with no correlation whatsoever. So running a standard correlation test should yield p values that are uniformly distributed on [0,1]. As it does (histogram on the left below).

However, suppose we first smooth each series and apply the correlation test to the smoothed data. Something surprising appears: since we have removed a lot of variability from the data, we get p values that are far too small. Our correlation test is heavily biased. So we will be too certain of any association between the original series, which is what Briggs is saying.

The question really hangs on whether we use the smoothed data for forecasting, in which case smoothing is valid, or whether we include it as an input in some analytical algorithm, in which case removing variability will simulate higher certainty in our data than is warranted. This unwarranted certainty in input data carries through to end results and needs to be accounted for, otherwise all inferences will be too certain. (And of course we will also get too small prediction intervals if we use a model based on "inflated certainty" for forecasting.)

n.series <- 1e4
n.time <- 1e2

p.corr <- p.corr.smoothed <- rep(NA,n.series)
set.seed(1)
for ( ii in 1:n.series ) {
    A <- rnorm(n.time)
    B <- rnorm(n.time)
    p.corr[ii] <- cor.test(A,B)$p.value
 p.corr.smoothed[ii] <- cor.test(lowess(A)$y,lowess(B)$y)$p.value
}

par(mfrow=c(1,2))
hist(p.corr,col="grey",xlab="",main="p values\nunsmoothed data")
hist(p.corr.smoothed,col="grey",xlab="",main="p values\nsmoothed data")

Answer 2

Claiming that smoothing is inappropriate for a modeling analysis condemns it to having higher mean square error than it otherwise might. Mean square error or MSE can be decomposed into three terms, a square of a value called ``bias'', a variance, and some irreducible error. (This is shown in the citations below.) Excessively smoothed models have a high bias, even if they have low variance, and too rough models have high variances, and low bias.

There's nothing philosophical about this at all. It is a mathematical characterization. It does not depend upon the character of the noise or the character of the system.

See:

http://scott.fortmann-roe.com/docs/BiasVariance.html

https://galton.uchicago.edu/~lafferty/pdf/nonparam.pdf

http://www.inf.ed.ac.uk/teaching/courses/mlsc/Notes/Lecture4/BiasVariance.pdf (This has the derivation of the decomposition.)

http://www.cs.columbia.edu/~blei/fogm/2015F/notes/regularized-regression.pdf (Blei does the same in a different way, and brings in what happens when one tries to predict.)

Classical statistics almost always insisted upon unbiased estimates. In 1955, statistician Charles Stein of Stanford showed that there were combinations of unbiased estimators which had lower MSE for important special cases, notably what became called the JAMES-STEIN ESTIMATORS. Bradley Efron wrote a very approachable text about this revolution in insight: http://statweb.stanford.edu/~ckirby/brad/other/Article1977.pdf