I'm analyzing the distribution of network latency. The median upload time (U) is 0.5s. The median download (D) time is 2s. However, the median total time (for each data point, T = U + D) is 4s.
What conclusions could be drawn knowing that the median of the sum is much greater than the sum of the medians of the addends?
Just out of curiosity for stats, what would it mean if this question replaced median with average?
Medians are not linear, so there are a variety of circumstances under which something like that (i.e. $\text{median}(X_1)+\text{median}(X_2)<\text{median}(X_1+X_2)$) might happen.
It's very easy to construct discrete examples where that sort of thing occurs, but it's also common in continuous situations.
For example it can happen with skewed continuous distributions - with a heavy right tail, the medians might both be small but the median of the sum is "pulled up" because there's a good chance that one of the two is large, and a value above the median is typically going to be far above it, making the median of the sum larger than the sum of the medians.
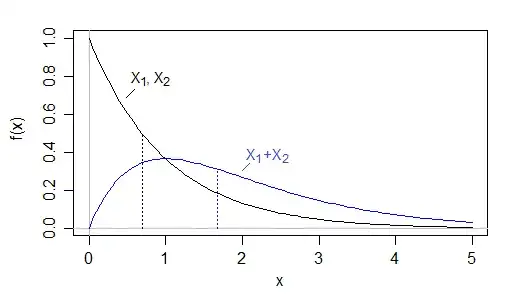
Here's an explicit example: Take $X_1,X_2 \, \stackrel{\text{i.i.d.}}{ \sim} \operatorname{Exp}(1)$. Then $X_1$ and $X_2$ have median $\log(2) \approx 0.693$ so the sum of the medians is less than $1.4$, but $X_1+X_2\sim \operatorname{Gamma}(2,1)$ which has median $\approx 1.678$ (actually $ -W_{-1}(-\frac{1}{2 e}) - 1$ according to Wolfram Alpha)
