The aim is to estimate an error on a stochastic event rate dynamically.
This Question points in the same direction, I am interested in a theoretical extension.
I read out the event counter second-wise, every black $1$ is a counted event (new events over time, see the plot below).
During the measurement I am estimating the event rate, so as more statistics is accumulated, mean event rate (red) should asymptotically become more accurate.
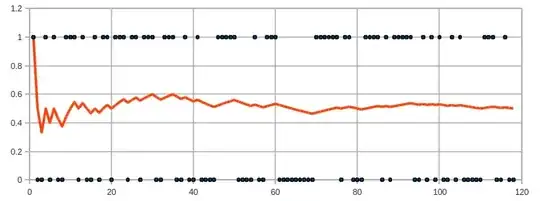
As one can see, the mean value oscillates around true value of 0.5,
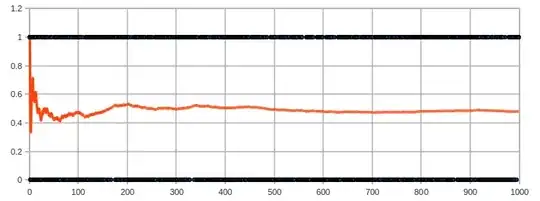
even after one order of magnitude more events collected.
Practical question: How can one calculate the number of events needed to estimate the mean value to a maximum error ($0.5\pm \sigma$)? - answered (?) here
Theoretical question: Can this oscillation be described analytically? Can you suggest further reading?
The events are radiation counts, so they are uncorrelated, may by Poisson-distribution applied?
Addendum:
Idealized first approximation - every 10th event is non-zero:
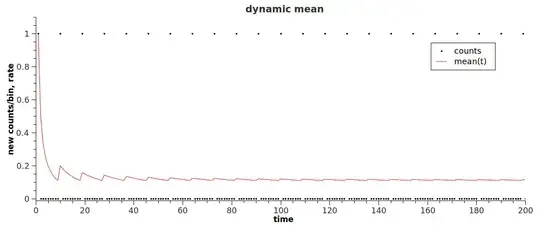
May be this curve is superimposed with the realer-life example above, is any techniques of partitioning in arbitrary functions applicable here?