I am currently working on a statistical project where I need to estimate a conditional expectation $E[Y|X=x_i]$ using the Nadaraya-Watson estimator. For doing that, I have the sample $(x_1,y_1),...,(x_n,y_n)$, where $n=14$, and I have chosen the bandwidth $h$ such that : $h = n^{-\frac{1}{5}}=0.5899$, given that the common rule of thumb is to have $h \propto n^{-\frac{1}{5}}$ for optimality.
However, I do not get in what sense that $h$ is optimal. Indeed, I am using R, the ksmooth function with a normal kernel : ksmooth(X,Y,"normal",bandwidth=h).This is what I get if I choose such a $h$:
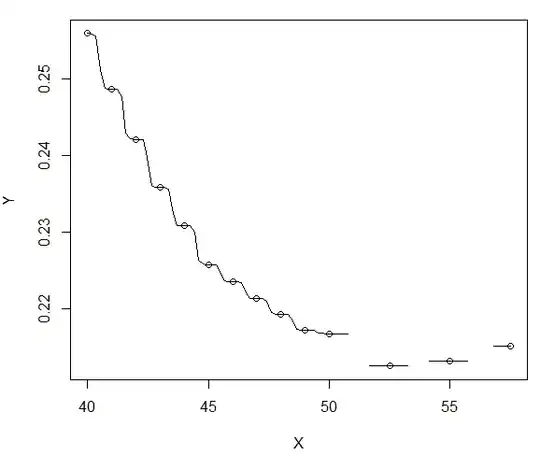
While if for example I choose $h$ equal to 3 (so around 5 times bigger), I get a way smoother curve, which is what really interests me:
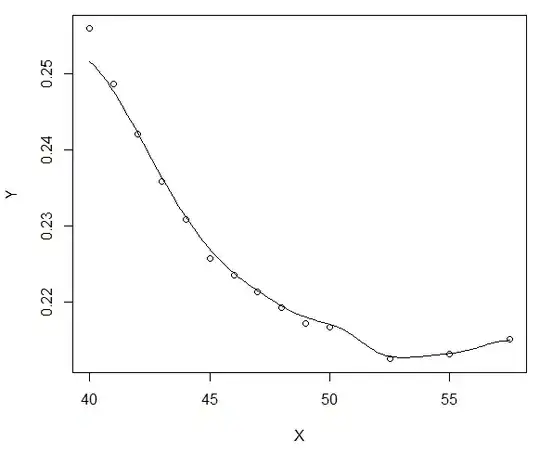
Could someone explain me in what sense having $h \propto n^{-\frac{1}{5}}$ is "optimal"?
What am I sacrificing if I choose a $h$ bigger than the "optimal" one: accuracy, convergence speed, etc.?
I greatly appreciate, thank you very much.