I am trying to fit an ARIMA model and I have already evaluated a few variations which I finally selected ARIMA(1,1,3) model. The residuals seems to be uncorrelated and all the lags are significant. However, in this model and even in all the others I tried, the normality condition for residuals is always violated and they look like this when plotted against normal distribution. 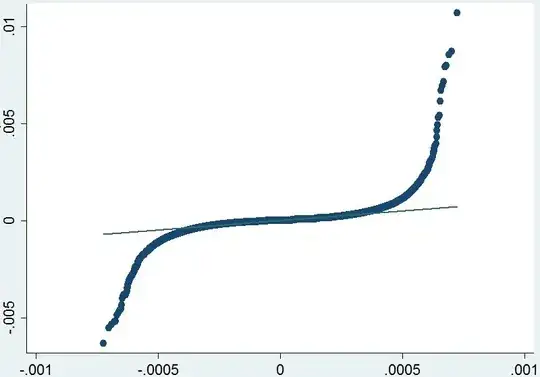
Should I transform my data somehow? I have already used natural log and first differencing in order to make the data stationary or can I ignore the assumption when I have a lot of observations (1,5M) ?