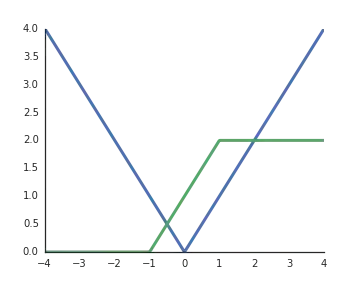
Why are activation functions of rectified linear units (ReLU) considered non-linear?
$$ f(x) = \max(0,x)$$
They are linear when the input is positive and from my understanding to unlock the representative power of deep networks non-linear activations are a must, otherwise the whole network could be represented by a single layer.