4

Background: In some cognitive psychology research areas N-alternative forced choice tasks are common. The most common of these is a two alternative forced choice (2AFC). This usually takes the form of participants being given a stimulus and asked to make one of two judgement, e.g. the target stimuli is present/absent, the stimulus on the left is the same/different than the the one on the right, etc. Designs in which the experimental data is from a 2AFC but there is only one data point per subject are rare, but do exist, e.g. some eye-witness identification research. Since the dependent variable (correct/incorrect) is binary, these experiments are reasonable places to use logistic regression.

My question is this: since chance performance is 50% in a 2AFC trial, is it still reasonable to use the standard logistic link function? Specifically, the logistic function has a minimum value approaching 0% correct, but in practice participants in a 2AFC should be correct at least 50% of the time due to chance. I imagine the following case in which it may present a problem: an independent variable is assessing the difficulty of the discrimination (e.g. difficulty 1, easy - 5, hard; please note this is introduced in ordinal terms only for ease of comprehension - for the sake of this discussion consider this variable as being interval) - participants got 50% correct at 5 and 4, 75% correct at 3, 85% correct at 2, and 99% correct at 1. Would using a standard logistic link function cause us to underestimate the slope? [I think so, but please correct me if I'm wrong, see below]

Edit: Those who have answered my question so far have expressed that the way in which I set up the problem was unclear. I'm providing the sample below to help clear things up.

library(psyphy)
make.data <- function(zero,one)
    {
        return(c(rep(0,zero),rep(1,one)))
    }
center <- function(x) {return(scale(x,scale=FALSE))}
logit.data <- data.frame(Score=c(make.data(50,50),make.data(50,50),make.data(25,75),make.data(15,85),make.data(1,99)), Difficulty=rep(5:1,each=100))
logit.data$Difficulty2 <- center(logit.data$Difficulty)^2
standard <- glm(Score~center(Difficulty),data=logit.data,family=binomial) #standard link function
standard.2 <- glm(Score~center(Difficulty)+Difficulty2,data=logit.data,family=binomial) #standard link function, but better with a quadradic
revised.link <- glm(Score~center(Difficulty),data=logit.data,family=binomial(mafc.logit(2)))
AIC(base)
AIC(base.2)
AIC(revised.link)
coef(base)
coef(base.2)
coef(revised.link)
#plot
plot(diffs,plogis(coef(standard)[1] +coef(standard)[2]*center(diffs)),xlab="Difficulty",ylab="Pr(Correct)",ylim=c(0,1),col="blue",type="l");abline(.5,0,col="Orange");lines(diffs,plogis(coef(standard.2)[1]+coef(standard.2)[2]*center(diffs)+coef(standard.2)[3]*center(diffs)^2),col="Cyan");lines(diffs,(p2afc(coef(revised.link)[1]+coef(revised.link)[2]*center(diffs))),col="Green");lines(5:1,c(.55,.60,.75,.85,.99),col="Black")

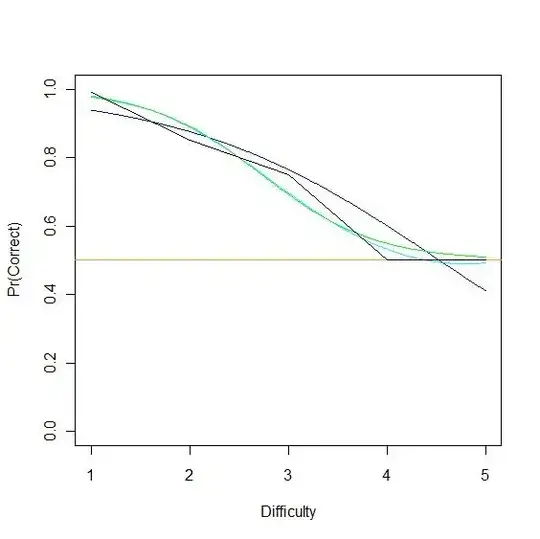
alt text

In the above image the orange horizontal line marks 50% correct responses. The jagged black line represents the data supplied to the estimation equation (note the values for 4 and 5 disappear behind the orange 50% marker). The blue line is the equation produced by a standard logistic link. Note that it estimates below 50% accuracy when discrimination is most difficult (5). The cyan line is the standard logistic link with a quadratic term. The green line is a non-standard link that takes into account that the data comes from a 2AFC experiment where performance is very unlikely to fall below 50%. Note that the AIC for a model fit using a non-standard link function is superior to the standard logistic link function. Also note that the slope for the standard equation is less than the slope for the standard equation with the quadratic term (which more accurately reflects the real data). Thus, using a logistic function blindly on 2AFC data does (at least) appear to underestimate the slope.

Is there a problem with my demonstration that means that I am not seeing what I think I am seeing? If I'm correct, then what other consequences (if any) are there of using the generic logistic function with 2AFC data [presumably extensible to NAFC cases]?

russellpierce
  • 17,079
  • 16
  • 67
  • 98

2 Answers2

1

My question is this: since chance performance is 50% in a 2AFC trial, is it still reasonable to use the standard logistic link function?

yes.

Think of it this way: suppose you fit a logistic regression where your $y$ variable takes value 1 if subject i has flue, 0 otherwise.

So long as neither $y_i=1$ nor $y_i=0$ are rare events, then flue incidence (i.e. $n^{-1}\sum_{i=1}^ny_i$) is not relevant, it will be absorbed by the intercept of your model.

but in practice participants in a 2AFC should be correct 50% of the time due to chance

if this statement is true and all your exogenous variables have been de-meaned, then, you can expect your estimated constant to be $logit^{-1}(0.5)\approx0.05$

Best,

user603
  • 21,225
  • 3
  • 71
  • 135
  • I'm not sure I understand your answer. I think you are saying I do not need to specify a link function because the intercept of my model will adjust based on the data and effectively account for the fact that at high difficulties people will not be able to perform the task. Is that correct? If so, how does this prevent a flattening of the slope estimate due to the same values at difficulties 4 and 5? I may need a less technical explanation (if possible). – russellpierce Aug 08 '10 at 18:40
  • *I'm not sure I understand your answer...Is that correct?* yes The limitation with the logit is one of symmetry; going back to your example, you force the slope between 4 and 5 to be the same as the slope between 1 and 2. If symmetry is a problem, you might want to try a complementary log-log link (not implemented in LMER). – user603 Aug 08 '10 at 20:09
  • I think your example is somewhat boggus in that the variable "difficulty of the discrimination" is really a ordinal scale and should be introduced in your regression as such. The problem you would have in this case would be due to you wrongly introducing "difficulty of the discrimination" as a continuous predictor when it is not, not to the logit link per see. – user603 Aug 08 '10 at 20:17
  • @kwak: I introduced it as an ordinal because it is easier to describe that way. Difficulty of discrimination in many of these experiments is a quantifiable ratio scale variable, e.g. contrast or noise introduced to the signal. – russellpierce Aug 08 '10 at 21:29
  • @kwak: Does your suggestion to use a complementary log-log link still apply given that the IV is an interval scale variable? – russellpierce Aug 08 '10 at 21:36
  • @drknexus#1:> understood, but the mishandled ordinal scale was what was causing the expected behavior of the logit seem inappropriate, so i pointed it out. @drknexus#2:> what you mean by "IV"? – user603 Aug 08 '10 at 21:46
  • I'm not sure what you mean by "mishandled ordinal scale". Is the problem that the data itself is not spread out in a continuous fashion? I'd like to simulate this with continuous data, but I can't think of a way of generating values that don't beg the question. Any ideas? By IV I meant "independent variable"/"predictor", sorry for using shorthand. – russellpierce Aug 08 '10 at 23:19
1

I don't see how the question in your example is sensible. The slope of the values is the slope of the values. Using a logistic link function then you get the slope of the logit of the values. There's no under or overestimating.

The more interesting case in your (our) field is that of interactions in accuracy. You might want to read Dixon (2008) as one of the more recent papers on this problem. It also addresses many of your fundamental concerns.

In general, in cognitive and perceptual psychology a logit link function is better than any other standard link. If you want to know the true effects of your independent variables, (i.e. whether they interact or are additive, whether they are linear or curvilinear) then you would need to know better the true underlying model. Since you probably don't know that logistic regression is probably better than almost anything else and vastly better than just analyzing meaned accuracy scores.

The primary consequence of doing this is contradicting other findings where mean accuracy scores were put into an ANOVA or regression.

* EDIT*

Now that you've added some data it looks like you're trying to model a floor effect that shouldn't be there. At some point the task becomes impossible. It looks like that already happened at your level 4 difficulty. Modelling level 5 is useless. What if you had a level 6 or 7 difficulty?

It looks like a logistic will fit points 1-4 pretty well.

And, you should be looking at residuals to assess fit, not just the curves overlaid.

John
  • 21,167
  • 9
  • 48
  • 84
  • The example is a case where a single predictor linear equation, though rationally sound given the dataset, will provide a suboptimal solution to the problem. If in the example case you fit a quadratic as well you'd likely get an improved model fit would you not? The improved model fit wouldn't be a consequence of some underlying real quadratic effect of the IV, just that you'd hit a measurement floor. – russellpierce Aug 08 '10 at 22:06
  • I'll take a look at Dixon - thanks for the reference - it looks right up my alley. The alternative link I was imagining was an explicitly 2AFC link, e.g. mafc.logit(2) in the psyphy package of R. – russellpierce Aug 08 '10 at 22:14
  • Doesn't the AIC adequately assess model fit for these purposes? I only provided the curves to demonstrate/visualize what is going wrong. The problem isn't simply because the floor has been hit. To convince yourself of this, try difficulty 4 at 60% and 5 at 55%. The logistic curve still is dropping down into "impossible" territory. Yes, it might be nice to not assess difficulty levels where the task is "impossible" but you don't always know where those levels are going to be in advance of preliminary data collection. – russellpierce Aug 09 '10 at 07:09
  • My take on it is this: the problem we are observing is analogous to why using percentages as linear predictors is fine until you start reaching the extremes of the percentages - the logistic function and a linear function are reasonably matched until you get upwards of 80%. Likewise, in the low end here the basic logistic function is a reasonable match until the probability of correct answers starts dipping below 60% or so. Then you find yourself in part of the curve where the logistic function is predicting a continued drop off in accuracy whereas the 2AFC function predicts a leveling. – russellpierce Aug 09 '10 at 07:15
  • As to your first comment, I see that you have a good answer about how to look at the residuals from another posted question but you still don't have why. AIC, log-likelihood, etc. all tell you how good you fit is but they don't tell you the nature of the fit.. it's like comparing SD and histograms for looking at variability. They both tell you about variability. – John Aug 09 '10 at 12:22
  • As to your second problem, no. Of course the chance end of the scale can be variable but pretty much anyone who's extensively studied SAT curves can attest (Ratcliff, Lappin, Pachella) that there isn't much useful variability in the chance end of the scale. It just ditches catastrophically. All of the above names work with models other than just logistic to come to this. It's also a simple measurement issue. At the low end of the scale you have a good measure of error. At the high end you don't. So, you can trust your low accuracy measures better. – John Aug 09 '10 at 12:22
  • And your comment about imagining that accuracy started going up... typically in one curve you want to model a single psychological process. I doubt accuracy increasing after difficulty exceeded some point does that. It would be tapping a different process... or just be some chance variation. – John Aug 09 '10 at 12:24
  • BTW, to really understand modelling accuracy over a change in difficulty you might want to look at the SAT literature since it does exactly that. – John Aug 09 '10 at 12:25
  • I understand now why looking at the residuals directly might be useful. In this case it would indicate where the model was beginning to fail. I don't think I said that accuracy should go up at increased levels of difficulty (although that is what the quadradic model would imply). I just said that accuracy in 2AFC will hit a floor after which it will not continue to go down as a function of increased difficulty. This is a result of a fairly simple psychological process interacting with the 2AFC design. – russellpierce Aug 09 '10 at 17:16
  • I'll grant that in the current model, it may make sense simply to drop the high difficulty levels that are giving the logistic model problems. Though if, as you say, you can trust your low accuracy measures better, then aren't you are advocating I throw away the very observations that should be most trusted? I'll shelve the question for now and may come back to it in a couple months after I've had time to look further at the literature you've cited. – russellpierce Aug 09 '10 at 17:25