When AIC and Adjusted $R^2$ lead to different conclusions

Question

I hope it's okay to ask theoretically driven R questions here. R has given me the following results from my 'tournament of models'. All models are entirely distinct except from 3 basic control variables. It's clear to me that Model 3 (third column) is the best performing. My concern is that Model 4 has such as low $R^2$, despite having a low AIC. How would you theoretically explain why a model has low and AIC but also a low $R^2$?

Secondly, imagine I went to add the variables from Model 4 into each of the other models and note the reduction of AIC scores. If the reductions in AIC is different across each model, what does this suggest?

Should it be the case that the inserted variables do better when inserted into a very different thereotical model?

[For info I consulted this other thread but decided to create my own since I was still unclear of the distinction between goodness of fit and explanatory power.] The 'best' model selected with AICc have lower $R^2$ -square than the full/global model

Answer 1

$R^2$ and AIC are answering two different questions. I want to keep this breezy and non-mathematical, so my statements are non-mathematical. $R^2$ is saying something to the effect of how well your model explains the observed data. If the model is regression and non-adjusted R^2 is used, then this is correct on the nose.
AIC, on the other hand, is trying to explain how well the model will predict on new data. That is, AIC is a measure of how well the model will fit new data, not the existing data. Lower AIC means that a model should have improved prediction.
Frequently adding more variables decreases predictive accuracy and in that case the model with higher $R^2$ will have a higher (worse) AIC. A nice example of this is in "Introduction to Statistical Learning with R" in the chapter on regression models including 'best subset' and regularization. They do a pretty thorough analysis of the 'hitters' data set. One can also do a thought experiment. Imagine one is trying to predict output on the basis of some known variables. Adding noise variables to the fit will increase R^2, but it will also decrease predictive power of the model. Thus the model with noise variables will have higher $R^2$ and higher AIC.

Answer 2

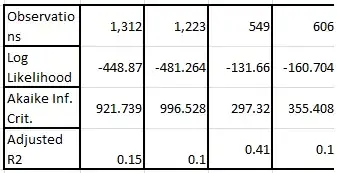
Which model is better is

1) not chosen using AIC as AIC only compares fit functions for the same data set.

2) not chosen using $R^2$ naively. For example, if two variables are supposed to be uncorrelated, then the least $R^2$ belongs to the better model.

3) $R^2$ is only proper to use (adjusted or not) if the conditions for OLS (ordinary least squares) and/or maximum likelihood are met. Rather than state what all the OLS conditions are, as there are multiple sets of rules all of which result in OLS conditions, let us state what they are not, that is, if we have very non-normal far outliers for the x-axis variable, and low $R^2$ values, the $R^2$ value is not worth the paper it is written on. In that case, we would 3a) trim the outliers or 3b) use $rs^2$ (Spearman's rank sum correlation), 3c) not use OLS or maximum likelihood, but use Theil MLR regression or an inverse problem solution, and not try to use r-values.

4) One can use 4a) Pearson Chi-Squared, 4b) t-testing for x-axis histogram categories, or if needed because of non-normality of residuals: one-sided Wilcoxon testing, and 4c) also one can test how compact each set of residuals is by comparing variances using Conover's non-parametric method (in virtually all cases) or Levene's test if normally distributed residual testing is good enough. Similarly one can use 4d) ANOVA with partial probabilities of the relevance of each fit parameter (bottoms up) AND simplify models by including all available parameters and then eliminate all unnecessary parameters by throwing in everything and eliminating parameters that are unlikely to contribute (top-down). Both top-down and bottoms-up are needed to finally decide on what model is the "best" keeping in mind that the residual structure may not be very amenable to using ANOVA and that our parameter values will most likely be biased by using OLS.

BEFORE we do believe any of the above, we should check our x-axis and y-axis variables and/or combinations of parameters to make sure we have "nice" measurements. That is, we should look at linear versus linear plots, log-log plots, exponential-exponential plots, reciprocal-reciprocal, square-root and square-root plots and all mixtures of the above and others: log-linear, linear-log, reciprocal-exponential etc., to determine which is going to produce the most normal conditions, the most symmetric residual pattern, the most homoscedastic residuals, etc., and then only test models that make sense in the "nice" context.

5) Stuff I left out or do not know about.

Answer 3

How would you explain why a model has low and AIC but also a low R2?

This is because they are different measures.

• $R^2$ is a measurement of training error.
• $AIC$ is an estimate of the test error that takes bias and variance into account.

Recall the equations for both: $$ R^2 = 1 - RSS / TSS$$ $$ AIC = \frac{1}{n\hat{\sigma}^2}(RSS + 2d\hat{\sigma}^2)$$

*$d$ is the number of predictors in the model.

In a situation where an increase in bias leads to a relatively small decrease in variance, you can see that a model with high bias (low value of $d$) might have a low $AIC$ and low $R^2$ compared to a more complex model with low bias (high value of $d$) and a high $R^2$.

---

If the reductions in AIC is different across each model, what does this suggest?

This suggests that some predictors, or subsets of predictors, reduce $RSS$ more than others.

---

Should it be the case that the inserted variables do better when inserted into a different model?

Perhaps. There might be collinearity or multicollinearity between your predictors.

Assume a predictor has a significant relationship with the response. Let's also assume we have 2 models: one where collinearity exists between this predictor and the others in the model, and another where no collinearity exists between this predictor and the others.

Inserting the predictor into the first model will yield a smaller increase in performance than inserting it into the second model. This is because the collinear predictors in the first model will already have 'explained' some of the inserted predictor's relationship with the response.

Answer 4

AIC has no "absolute scale": for models $m_i$ fit from data $x$ the model AIC is only ever calculated up to an unknown constant, ie. $\text{AIC}_i = \text{AIC}^{\text{true}}_{i} - C_x$ where $C_x$ is an unknown constant that depends on observations $x$. Since $C_x$ is common between models fit to the same data set $x$ we can just use $\Delta_{ij} = AIC_i - AIC_j = \text{AIC}^{\text{true}}_{i} - C_x - \text{AIC}^{\text{true}}_{j} + C_x = \text{AIC}^{\text{true}}_{i} - \text{AIC}^{\text{true}}_{j}$ for model comparison. If you fit models using different data sets $x$ and $x'$ then you've got two different $C_{x_i}$ and $C_{x_j}$, so the constants don't cancel and $\Delta_{ij} = \text{AIC}^{\text{true}}_{i} - C_{x_i} - \text{AIC}^{\text{true}}_{j} + C_{x_j}$ is meaningless.

From this viewpoint we can expect to low $R^2_i$ and also low $\text{AIC}_i$ when $C_{x_i}$ is sufficiently small relative to the other $\text{AIC_j}$ and $C_{x_j}$. IIRC, the $C_{x_i}$ are proportional to the likelihood of the observations, which is a product of probabilities for each observation in your data; I don't think it's an accident that your smallest AIC correspond to the fewest observations.