7

I have a multivariate dataset for which I have only a table including the cross-wise Euclidean distances between all points and a list giving the assignment of each point to one of several clusters. Can I use those data to calculate the within-group sum of squares within each of the clusters?

EDIT 1

Let me add an example on how I would do it, and to further explain what I want to do. Say I have the following data. I have six samples which are attributed to two clusters: S1-S3: Cluster 1 S4-S6: Cluster 2

Additionally, I have the distances between samples:

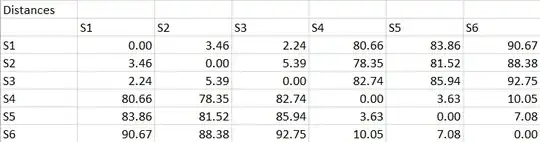
enter image description here

Now, if I want to calculate the sum of squares within Cluster 1, I would have the following values for the distances D: D(S1, S2) = 3.46 D(S1, S3) = 2.24 D(S2, S3) = 5.39

The mean of this would be D* = 3.70 According to the normal equation for the sum of squares TSS = sum((Di - D*)^2), as adapted from linear regression, this would lead me to TSS = sum(12.00, 2.13, 2.86), so TSS(Cluster 1) = 16.99

Equivalently: TSS(Cluster 2) = 20.66

But when I apply the same equations to the whole dataset (i.e. distances between all points) I get a TSS for the whole dendrogram of TSS(complete) = 23082.10

Finally, I would like to use all those calculations to deduce, how much of the observed variance is explained by the cluster-analysis. But if I would assume those results to be corrct (in this sense) then I would get an explained variance of only 0.16% (sum(16.99, 20.66)/23081.10).

So presumably, I make a mistake (the data were artifically produced to be explained by a dendrogram with two clusters, so the explained variance should probably be in access of 80%). Can anybody help me in this?

EDIT 2 Using the same data and the nice explanation here

I would then calculate the sum of squares per cluster as sum(Distances^2)/3. This would give me TSS(Cluster 1) = 15.33; TSS(Cluster 2) = 54.75. The total TSS of the dendrogram would then be TSS(total) = 10899.57, which would still yield an explained variance of only 0.6%.

Where am I making the mistake?

Community
  • 1
Manuel Weinkauf
  • 178
  • 1
  • 5
  • `multivariate dataset for which I have only a table including the cross-wise Euclidean distances`. Is that you have the square matrix of distances between all the points (instead of the original pointsXvariables data)? Then yes, you can. – ttnphns Mar 06 '15 at 18:35
  • @ttnphns Yes, this is exactly what I mean. The question is then, how I do it. Can I just us the normal euqation sum(yi-y*)^2, with yi as individual distance measures and y* as mean of distances within the cluster? Or is there any further problem with that. – Manuel Weinkauf Mar 09 '15 at 09:44
  • 1
    Please see the 1st paragraph [here](http://stats.stackexchange.com/a/81494/3277). So, for each cluster, consider its distance submatrix (of squared distances) and compute the within-cluster sum of squares of deviations from the cluster centroid. – ttnphns Mar 09 '15 at 10:05
  • @ttnphns Thanks for the link. Alas, see EDIT 2, I am still unable to do what I want to do. It's probably a stupid mistake in understanding the method. I guess you see it right away. – Manuel Weinkauf Mar 09 '15 at 10:46
  • 1
    I didn't check your calculations. Are you doing it right? If you have n points and nXn squared distances between them you should divide the sum of n(n-1)/2 distances by n. And what are you calling `the explained variance`? Isn't it the between-cluster variance and not the within-cluster (which is akin "error")? SStotal = SSwithin + SSbetween. – ttnphns Mar 09 '15 at 11:13
  • @ttnphns Yes, the sum of squares within the cluster I calculated as you state, by summing the n(n-1)/2 distances and deviding them by n (I used the squared distances, that is to say). But how would I then calculate the between-cluster sum of squares? – Manuel Weinkauf Mar 09 '15 at 14:55
  • Did you read my previous comment to the end? Compute SStotal (all points considered as one cluster). Compute SScluster for each separate cluster. The sum of the latter over all clusters is SSwithin. Subtract. [If you think in terms of variance (rather than SS), - then the df for SSbetween is k-1 and df for SSwithin is N-k (N being the total sample size and k is the number of clusters. See this site or internet for "Calinski–Harabasz clustering criterion"]. – ttnphns Mar 09 '15 at 16:45
  • @ManuelWeinkauf see this [thread](http://stats.stackexchange.com/questions/86645/variance-within-each-cluster/165049#165049) – Antoine Aug 06 '15 at 21:35
  • 1
    This question is answered in http://stats.stackexchange.com/q/237792/3277 thread where all the principal formulas are given – ttnphns Oct 04 '16 at 18:34

0 Answers0