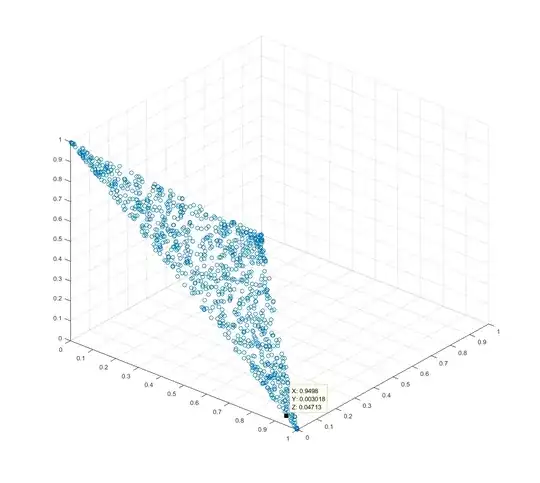
It is common to use weights in applications like mixture modeling and to linearly combine basis functions. Weights $w_i$ must often obey $w_i ≥$ 0 and $\sum_{i} w_i=1$. I'd like to randomly choose a weight vector $\mathbf{w} = (w_1, w_2, …)$ from a uniform distribution of such vectors.
It may be tempting to use $w_i = \frac{\omega_i}{\sum_{j} \omega_j}$ where $\omega_i \sim$ U(0, 1), however as discussed in the comments below, the distribution of $\mathbf{w}$ is not uniform.
However, given the constraint $\sum_{i} w_i=1$, it seems that the underlying dimensionality of the problem is $n-1$, and that it should be possible to choose a $\mathbf{w}$ by choosing $n-1$ parameters according to some distribution and then computing the corresponding $\mathbf{w}$ from those parameters (because once $n-1$ of the weights are specified, the remaining weight is fully determined).
The problem appears to be similar to the sphere point picking problem (but, rather than picking 3-vectors whose $ℓ_2$ norm is unity, I want to pick $n$-vectors whose $ℓ_1$ norm is unity).
Thanks!
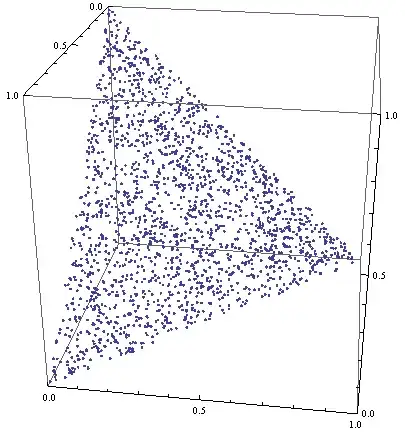
![[3D point plot 2]](../../images/3822980239.webp)