7

I know I mess up different things. However I want to get better understanding what is motivation behind logistic regression.

$p(y_i=1|x_i)=(1+e^{-x_iw})^{-1}$

and according to OLS

$S(w)=\sum_{i}^{}(y_i-\hat{y_i})^2$,where $y \in \{1,0\}$.

What if $\hat{y_i}=p(y_i=1|x_i)$ and estimate $w$ by finding minimum to $S(w)$.

Why this is incorrect approach?

com
  • 255
  • 2
  • 9
  • 2
    If you want to use OLS techniques, a (much) better way to study this relationship is to regress $x_i$ against $y_i$, rather than $y_i$ against $x_i$. As I recall, Hosmer and Lemeshow even recommend that as a reality check and way to get starting coefficients for fitting a logistic regression. – whuber Mar 05 '15 at 19:28
  • See https://stats.stackexchange.com/questions/326350/what-is-happening-here-when-i-use-squared-loss-in-logistic-regression-setting – kjetil b halvorsen Nov 20 '20 at 13:15

2 Answers2

4

I think this essentially boils down to what cost function you want to minimize in order to estimate your parameter $w$. Typically, the negative log-likelihood is minimized for parameter estimation, what you have suggested looks like minimizing the Brier score. I think they would give very similar estimates for $w$ (edit: see comments).

edit: I should say, it is not an incorrect approach.

Jeff
  • 857
  • 6
  • 16
  • 2
    Agree up until the last sentence. They can give very different estimates for $w$. – Neil G Mar 05 '15 at 11:41
  • Now that I've thought about it some more, I think you are right. Thanks for pointing that out. – Jeff Mar 05 '15 at 11:50
3

What you are proposing is a linear probability model, i.e. an OLS regression for a binary dependent variable. The difference is that logit is a non-linear model whereas the linear probability model (as the name says) is linear. The difference is perhaps best understood graphically.

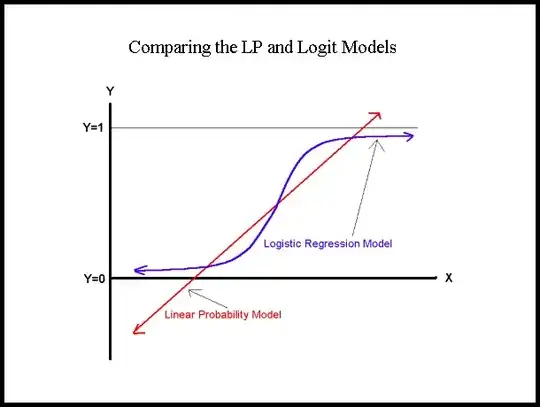
enter image description here

If you calculate the marginal effect of your logistic regression coefficients at the mean you will likely get very similar estimates than those from the OLS regression (in the graph that would be where the blue and the red line intersect or it will be at least close to it). The picture also shows nicely the problems of OLS in this case because you can see that it predicts outside the theoretical range, so it can give you predicted probabilities that are larger than one or smaller than zero. There are other advantages and disadvantages of either model (see for example these lecture notes for a summary).

In this sense there is nothing "wrong" with your approach. It just really depends on what you want to do with your model. If you are interested in estimating the marginal effect of your explanatory variables on the outcome probability then either is fine. If you want to do predictions then the linear probability model is not a good choice given that it's predicted probabilities are not bound to lie between zero and one.

Andy
  • 18,070
  • 20
  • 77
  • 100