As @whuber asked in the comments, a validation for my categorical NO. edit : with the shapiro test, as the one-sample ks test is in fact wrongly used. Whuber is correct: For correct use of the Kolmogorov-Smirnov test, you have to specify the distributional parameters and not extract them from the data. This is however what is done in statistical packages like SPSS for a one-sample KS-test.
You try to say something about the distribution, and you want to check if you can apply a t-test. So this test is done to confirm that the data does not depart from normality significantly enough to make the underlying assumptions of the analysis invalid. Hence, You are not interested in the type I-error, but in the type II error.
Now one has to define "significantly different" to be able to calculate the minimum n for acceptable power (say 0.8). With distributions, that's not straightforward to define. Hence, I didn't answer the question, as I can't give a sensible answer apart from the rule-of-thumb I use: n > 15 and n < 50. Based on what? Gut feeling basically, so I can't defend that choice apart from experience.
But I do know that with only 6 values your type II-error is bound to be almost 1, making your power close to 0. With 6 observations, the Shapiro test cannot distinguish between a normal, poisson, uniform or even exponential distribution. With a type II-error being almost 1, your test result is meaningless.
To illustrate normality testing with the shapiro-test :
shapiro.test(rnorm(6)) # test a the normal distribution
shapiro.test(rpois(6,4)) # test a poisson distribution
shapiro.test(runif(6,1,10)) # test a uniform distribution
shapiro.test(rexp(6,2)) # test a exponential distribution
shapiro.test(rlnorm(6)) # test a log-normal distribution
The only where about half of the values are smaller than 0.05, is the last one. Which is also the most extreme case.
if you want to find out what's the minimum n that gives you a power you like with the shapiro test, one can do a simulation like this :
results <- sapply(5:50,function(i){
p.value <- replicate(100,{
y <- rexp(i,2)
shapiro.test(y)$p.value
})
pow <- sum(p.value < 0.05)/100
c(i,pow)
})
which gives you a power analysis like this :
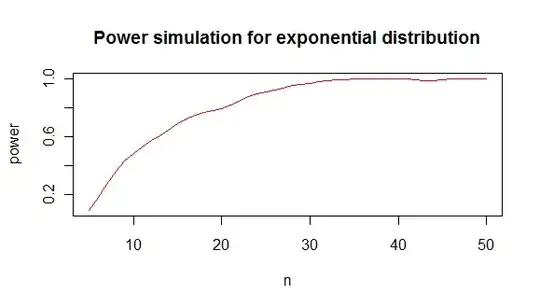
from which I conclude that you need roughly minimum 20 values to distinguish an exponential from a normal distribution in 80% of the cases.
code plot :
plot(lowess(results[2,]~results[1,],f=1/6),type="l",col="red",
main="Power simulation for exponential distribution",
xlab="n",
ylab="power"
)