What might be the general form of the equation can be fitted to the below scatter plot? The result should look like an smooth Z
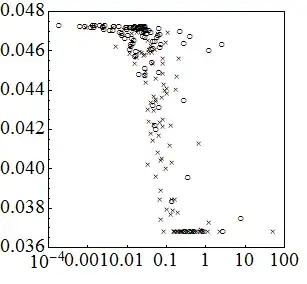
What might be the general form of the equation can be fitted to the below scatter plot? The result should look like an smooth Z

then, you might want to try additive models for quantile regressions (some pics/explanation here, and the $\verb+R+$ implementation here). These have various desirable properties: