QQ plot in Python

Question

I generated a qq plot using the following code. I know that qq plot is used to check whether the data is distributed normally or not. My question is what do the x and y axis labels indicate in qq plot and what is that r square value indicating??

  N = 1200
  p = 0.53
  q = 1000
  obs = np.random.binomial(N, p, size = q)/N

import scipy.stats as stats

z = (obs-np.mean(obs))/np.std(obs)

stats.probplot(z, dist="norm", plot=plt)
plt.title("Normal Q-Q plot")
plt.show()

I know that already there is a discussion about qq plot, but I couldnt understand the concept of despite of going through that discussion.

Answer 1

Macond's answer is accurate, however from the original post, I thought it might be helpful to simplify the verbiage a bit.

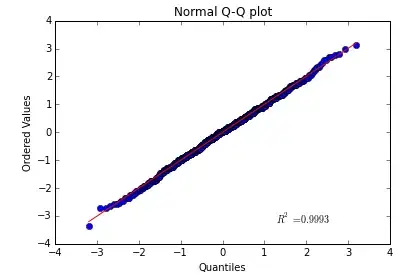
A Q-Q plot stands for a "quantile-quantile plot".

It is a plot where the axes are purposely transformed in order to make a normal (or Gaussian) distribution appear in a straight line. In other words, a perfectly normal distribution would exactly follow a line with slope = 1 and intercept = 0.

Therefore, if the plot does not appear to be - roughly - a straight line, then the underlying distribution is not normal. If it bends up, then there are more "high flyer" values than expected, for instance. (The link provides more examples.)

---

1. What do the x & y labels represent?

The theoretical quantiles are placed along the x-axis. That is, the x-axis is not your data, it is simply an expectation of where your data should have been, if it were normal.

The actual data is plotted along the y-axis.

The values are the standard deviations from the mean. So, 0 is the mean of the data, 1 is 1 standard deviation above, etc. This means, for instance, that 68.27% of all your data should be between -1 & 1, if you have a normal distribution.

2. What does the $R^2$ value mean?

The $R^2$ value is not particularly useful for this sort of plot. $R^2$ is typically used to determine whether one variable is dependent upon another. Well, you are comparing a theoretical value to an actual value. So there will necessarily be some sort of $R^2$. (E.g., even a random uniform distribution will have a moderately decent $R^2$.)

---

Lastly, there is a similar plot that is rarely used called the p-p plot. This plot is more useful if you are interested in focusing upon where the bulk of the data lies, instead of the extremes.

Answer 2

Y axis shows values of observed distribution and X axis, values of theoretical distribution.

Each point is a quantile. Let's say, if there were 100 points on the plot, the first point (the one on lower-left side) indicates an upper bound for an interval, and when ordered from smallest to largest, the smallest 1 percent of the data points of the corresponding distribution stays in this interval. Similarly, 2nd point is upper bound of an interval, where smallest 2 percent of data points from the distribution is located. This is the concept of quantile. But it is not limited to a case with 100 intervals, it is a general concept and you can have as many intervals as possible, then you will have that many quantiles describing boundaries of the intervals.

What is special about this plot is, each point's position determines actual value of the given quantile in both distributions, as corresponding value on the axis. Let's think as if there are 100 such points (quantiles) again, this plot tell that smallest 1 percent of data points from observed distribution is between ($ -\infty $, -3.5] and also smallest 1 percent of data points from theoretical distribution is between ($ -\infty $, -3.2]. This way you can see locations of each interval boundary's position in both distributions.

I used data points throughout my answer, like ordered data points etc. This refers to discrete distributions, but the concept can be generalized for continous distributions.

$R^2$ is a measure of how good the points fit to the red line. If both axes had the same distribution, all of the points would be exactly on the line and $R^2$ would equal 1. You can learn more about it in any text explaining linear regression.