Distribution of the maximum of two correlated normal variables

Question

Say I have two standard normal random variables $X_1$ and $X_2$ that are jointly normal with correlation coefficient $r$.

What is the distribution function of $\max(X_1, X_2)$?

Answer 1

Let $f_\rho$ be the bivariate Normal PDF for $(X,Y)$ with standard marginals and correlation $\rho$. The CDF of the maximum is, by definition,

$$\Pr(\max(X, Y)\le z) = \Pr(X\le z,\ Y\le z) = \int_{-\infty}^z\int_{-\infty}^z f_\rho(x,y)dy dx.$$

The bivariate Normal PDF is symmetric (via reflection) around the diagonal. Thus, increasing $z$ to $z+dz$ adds two strips of equivalent probability to the original semi-infinite square: the infinitesimally thick upper one is $(-\infty, z]\times (z, z+dz]$ while its reflected counterpart, the right-hand strip, is $(z, z+dz]\times (-\infty, z]$.

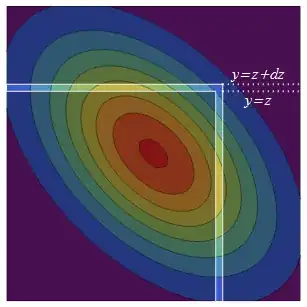
The probability density of the right-hand strip is the density of $X$ at $z$ times the total conditional probability that $Y$ is in the strip, $\Pr(Y\le z\,|\, X=z)$. The conditional distribution of $Y$ is always Normal, so to find this total conditional probability we only need the mean and variance. The conditional mean of $Y$ at $X$ is the regression prediction $\rho X$ and the conditional variance is the "unexplained" variance $\text{var}(Y) - \text{var}(\rho X) = 1-\rho^2$.

Now that we know the conditional mean and variance, the conditional CDF of $Y$ given $X$ can be obtained by standardizing $Y$ and applying the standard Normal CDF $\Phi$:

$$\Pr(Y \le y\,|\, X) = \Phi\left(\frac{y-\rho X}{\sqrt{1-\rho^2}}\right).$$

Evaluating this at $y=z$ and $X=z$ and multiplying by the density of $X$ at $z$ (a standard Normal pdf $\phi$) gives the probability density of the second (right-hand) strip

$$\phi(z)\Phi\left(\frac{z-\rho z}{\sqrt{1-\rho^2}}\right) = \phi(z)\Phi\left(\frac{1-\rho}{\sqrt{1-\rho^2}}z\right).$$

Doubling this accounts for the equi-probable upper strip, giving the PDF of the maximum as

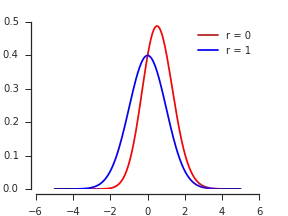
$$\frac{d}{dz}\Pr(\max(X,Y)\le z) = \color{blue}{2}\color{black}{\phi(z)}\color{darkred}{\Phi\left(\frac{1-\rho}{\sqrt{1-\rho^2}}z\right)}.$$

Recapitulation

I have colored the factors to signify their origins: $\color{blue}2$ for the two symmetrical strips; $\color{black}{\phi(z)}$ for the infinitesimal strip widths; and $\color{darkred}{\Phi\left(\cdots\right)}$ for the strip lengths. The argument of the latter, $\frac{1-\rho}{\sqrt{1-\rho^2}}z$, is just a standardized version of $Y=z$ conditional on $X=z$.

Here are plots of this density for a range of values of $\rho.$

Two dotted black curves in this figure provide references for the extreme cases:

For extremely positive $\rho,$ the density must approximate a Standard Normal distribution, because we are (to a good approximation) computing the larger of a standard normal variable $Z$ and a copy of itself.

For extremely negative $\rho,$ the density must approximate a Standard Half-Normal distribution, because the maximum of $Z$ and $-Z$ is $|Z|.$

Answer 2

According to Nadarajah and Kotz, 2008, Exact Distribution of the Max/Min of Two Gaussian Random Variables, the PDF of $X = \max(X_1, X_2)$ appears to be

$$f(x) = 2 \cdot \phi(x) \cdot \Phi\left( \frac{1 - r}{\sqrt{1 - r^2}} x\right),$$

where $\phi$ is the PDF and $\Phi$ is the CDF of the standard normal distribution.

$\hskip2in$