This is not a bug.
As we have explored (extensively) in the comments, there are two things happening. The first is that the columns of $U$ are constrained to meet the SVD requirements: each must have unit length and be orthogonal to all the others. Viewing $U$ as a random variable created from a random matrix $X$ via a particular SVD algorithm, we thereby note that these $k(k+1)/2$ functionally independent constraints create statistical dependencies among the columns of $U$.
These dependencies might be revealed to a greater or lesser extent by studying the correlations among the components of $U$, but a second phenomenon emerges: the SVD solution is not unique. At a minimum, each column of $U$ can be independently negated, giving at least $2^k$ distinct solutions with $k$ columns. Strong correlations (exceeding $1/2$) can be induced by changing the signs of the columns appropriately. (One way to do this is given in my first comment to Amoeba's answer in this thread: I force all the $u_{ii},i=1,\ldots, k$ to have the same sign, making them all negative or all positive with equal probability.) On the other hand, all correlations can be made to vanish by choosing the signs randomly, independently, with equal probabilities. (I give an example below in the "Edit" section.)
With care, we can partially discern both these phenomena when reading scatterplot matrices of the components of $U$. Certain characteristics--such as the appearance of points nearly uniformly distributed within well-defined circular regions--belie a lack of independence. Others, such as scatterplots showing clear nonzero correlations, obviously depend on choices made in the algorithm--but such choices are possible only because of the lack of independence in the first place.
The ultimate test of a decomposition algorithm like SVD (or Cholesky, LR, LU, etc.) is whether it does what it claims. In this circumstance it suffices to check that when SVD returns the triple of matrices $(U, D, V)$, that $X$ is recovered, up to anticipated floating point error, by the product $UDV^\prime$; that the columns of $U$ and of $V$ are orthonormal; and that $D$ is diagonal, its diagonal elements are non-negative, and are arranged in descending order. I have applied such tests to the svd algorithm in R and have never found it to be in error. Although that is no assurance it is perfectly correct, such experience--which I believe is shared by a great many people--suggests that any bug would require some extraordinary kind of input in order to be manifest.
What follows is a more detailed analysis of specific points raised in the question.
Using R's svd procedure, first you can check that as $k$ increases, the correlations among the coefficients of $U$ grow weaker, but they are still nonzero. If you simply were to perform a larger simulation, you would find they are significant. (When $k=3$, 50000 iterations ought to suffice.) Contrary to the assertion in the question, the correlations do not "disappear entirely."
Second, a better way to study this phenomenon is to go back to the basic question of independence of the coefficients. Although the correlations tend to be near zero in most cases, the lack of independence is clearly evident. This is made most apparent by studying the full multivariate distribution of the coefficients of $U$. The nature of the distribution emerges even in small simulations in which the nonzero correlations cannot (yet) be detected. For instance, examine a scatterplot matrix of the coefficients. To make this practicable, I set the size of each simulated dataset to $4$ and kept $k=2$, thereby drawing $1000$ realizations of the $4\times 2$ matrix $U$, creating a $1000\times 8$ matrix. Here is its full scatterplot matrix, with the variables listed by their positions within $U$:
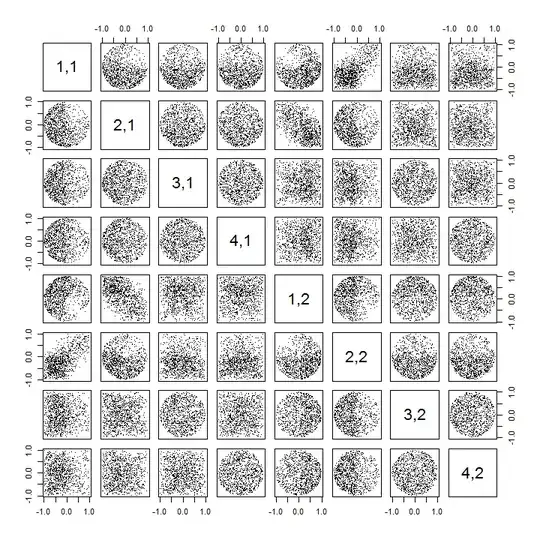
Scanning down the first column reveals an interesting lack of independence between $u_{11}$ and the other $u_{ij}$: look at how the upper quadrant of the scatterplot with $u_{21}$ is nearly vacant, for instance; or examine the elliptical upward-sloping cloud describing the $(u_{11}, u_{22})$ relationship and the downward-sloping cloud for the $(u_{21}, u_{12})$ pair. A close look reveals a clear lack of independence among almost all of these coefficients: very few of them look remotely independent, even though most of them exhibit near-zero correlation.
(NB: Most of the circular clouds are projections from a hypersphere created by the normalization condition forcing the sum of squares of all components of each column to be unity.)
Scatterplot matrices with $k=3$ and $k=4$ exhibit similar patterns: these phenomena are not confined to $k=2$, nor do they depend on the size of each simulated dataset: they just get more difficult to generate and examine.
The explanations for these patterns go to the algorithm used to obtain $U$ in the singular value decomposition, but we know such patterns of non-independence must exist by the very defining properties of $U$: since each successive column is (geometrically) orthogonal to the preceding ones, these orthogonality conditions impose functional dependencies among the coefficients, which thereby translate to statistical dependencies among the corresponding random variables.
Edit
In response to comments, it may be worth remarking on the extent to which these dependence phenomena reflect the underlying algorithm (to compute an SVD) and how much they are inherent in the nature of the process.
The specific patterns of correlations among coefficients depend a great deal on arbitrary choices made by the SVD algorithm, because the solution is not unique: the columns of $U$ may always independently be multiplied by $-1$ or $1$. There is no intrinsic way to choose the sign. Thus, when two SVD algorithms make different (arbitrary or perhaps even random) choices of sign, they can result in different patterns of scatterplots of the $(u_{ij}, u_{i^\prime j^\prime})$ values. If you would like to see this, replace the stat function in the code below by
stat <- function(x) {
i <- sample.int(dim(x)[1]) # Make a random permutation of the rows of x
u <- svd(x[i, ])$u # Perform SVD
as.vector(u[order(i), ]) # Unpermute the rows of u
}
This first randomly re-orders the observations x, performs SVD, then applies the inverse ordering to u to match the original observation sequence. Because the effect is to form mixtures of reflected and rotated versions of the original scatterplots, the scatterplots in the matrix will look much more uniform. All sample correlations will be extremely close to zero (by construction: the underlying correlations are exactly zero). Nevertheless, the lack of independence will still be obvious (in the uniform circular shapes that appear, particularly between $u_{i,j}$ and $u_{i,j^\prime}$).
The lack of data in some quadrants of some of the original scatterplots (shown in the figure above) arises from how the R SVD algorithm selects signs for the columns.
Nothing changes about the conclusions. Because the second column of $U$ is orthogonal to the first, it (considered as a multivariate random variable) is dependent on the first (also considered as a multivariate random variable). You cannot have all the components of one column be independent of all the components of the other; all you can do is to look at the data in ways that obscure the dependencies--but the dependence will persist.
Here is updated R code to handle the cases $k\gt 2$ and draw a portion of the scatterplot matrix.
k <- 2 # Number of variables
p <- 4 # Number of observations
n <- 1e3 # Number of iterations
stat <- function(x) as.vector(svd(x)$u)
Sigma <- diag(1, k, k); Mu <- rep(0, k)
set.seed(17)
sim <- t(replicate(n, stat(MASS::mvrnorm(p, Mu, Sigma))))
colnames(sim) <- as.vector(outer(1:p, 1:k, function(i,j) paste0(i,",",j)))
pairs(sim[, 1:min(11, p*k)], pch=".")