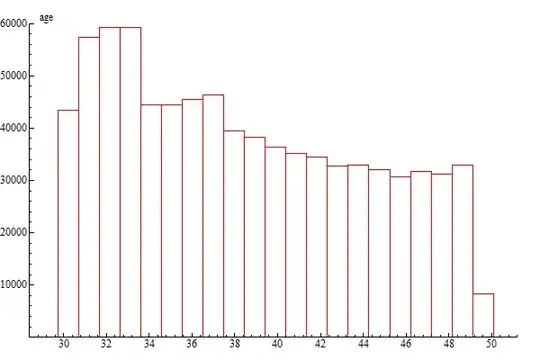
I have a cross-section of 100,000 individuals and information on their age. I suspect that there may be clustering by age or that the sample exhibits behavior that there would be two groups, the old and the young.
Is there a statistical test that tells me the location of the cut-off?
Looking at a histogram, I can eyeball it which occurs at 32 (not 42 incidentally..). But is there a way to test this?
Thanks so much!