42

I recently had a disagreement with a friend about minimizing the chance of dying in a plane due to a crash. This is a rudimentary statistics question.

He stated that he prefers to fly direct to a destination, as it decreases the probability that he will die in an airplane crash. His logic was that if the probability of a commercial airline crash is 1 in 10,000, flying on two planes to get to your destination would double your chance of death.

My point was that each time one flies on an airplane, it does not increase the likelihood that he will die in a future airplane crash. That is, each airplane flight is independent. Whether someone has flown on 100 planes that year or just 1, both fliers still have a 1 in 10,000 chance of dying in a plane crash on their next flight.

Another point I made: say your destination is 4 hours away. If you take a direct flight, you will be in the air, at risk of being in a crash, for 4 hours. Now say you take 4 different connecting flights, each flight about an hour long. In this scenario you will still be in the air for roughly 4 hours. Thus, whether you take the direct flight or save some money and take connecting flights, the amount of time you spend at risk is roughly equal.

My final point was that shorter flights have a lower rate of crashes. I just pulled that one out of nowhere. I've done zero research and have zero data to back that up but...it seems logical.

Who is in the right, and why? There's a lot at stake here.

Jeromy Anglim
  • 42,044
  • 23
  • 146
  • 250
Kyle
  • 531
  • 1
  • 4
  • 7
  • 6
    I looked at crash data a few years ago. As I recall, the *vast* majority of fatal crashes involve small planes, which therefore must be engaged in relatively shorter flights. Although there is indeed a lot at stake in commercial air travel--people's lives--that has to be balanced against the extremely low chance of accidents and the extremely high long-term chance of death or injury to those who would take alternative transportation, such as motor vehicles. – whuber Feb 14 '15 at 21:04
  • 3
    One way to break it down quite easily is to ignore the overall actual probability, and break it down into something simpler. Each time you fly, there is a chance of crashing. Assuming that flying more often is also associated with other correlates of crashing (e.g., flight length, taking off/landing), I think it is very safe to assume that a person who flies more is more likely to die in a plane crash. If someone was to fly 10,000 times in their lifetime, and another only once, who would you bet is more likely do die in a plane crash? – Behacad Feb 14 '15 at 21:18
  • 32
    Most crashes are at or close to an airfield, that is, inder take-off or landing (or even taxing on the airport). So minimizing number of takeoffs seems prudent! – kjetil b halvorsen Feb 14 '15 at 22:03
  • "1 in 10,000 chance of dying in their next plane crash"... that estimate of crash mortality rate seems absurdly low, perhaps you meant to talk about the probability that there would even be a crash? – Ben Voigt Feb 15 '15 at 01:52
  • 8
    Are your chances of dying in aircraft still 1/10000 if you never take any plane flights? – Lie Ryan Feb 15 '15 at 04:50
  • 5
    @Ben Please consult [the data.](http://www.transtats.bts.gov) In the US alone there are nearly 10 million commercial flights per year carrying almost a billion passengers. There are extremely few fatalities annually--[none in 2014,](http://en.wikipedia.org/wiki/List_of_accidents_and_incidents_involving_commercial_aircraft#2014) for instance and two in 2013. 1/10,000 is absurdly *high* by at least three orders of magnitude. – whuber Feb 15 '15 at 16:20
  • @whuber: And, now we need `p(crash | flight)` and to apply Bayes' theorem. Because question doesn't talk about `p(death | flight)` but `p(death | crash)`. – Ben Voigt Feb 15 '15 at 16:40
  • 1
    @Ben That's unnecessary: the data provide information that will enable you to estimate the quantities in the question directly. – whuber Feb 15 '15 at 16:42
  • 1
    @whuber: According to [this](http://www.planecrashinfo.com/cause.htm) the chance of dying in any crash is about 1 in 2. "Survival rate of passengers on aircraft ditching during controlled flight 53%" That satisfies common sense. Once again, quantity in the question is `p(death | crash)`. Your quoted data has N(death) but doesn't have N(crash), and when I visit your link all the ongoing links like "Aviation Accident Statistics" are broken. – Ben Voigt Feb 15 '15 at 16:46
  • 2
    @Ben Upon re-reading the question, I understand what you mean: given the context, I interpreted the event "dying in their next plane crash" just to be an awkward way of meaning "dying in their next flight due to a crash." We could indeed read it literally, as you have, but I think that leads to a discussion of something that is of little relevance to any airline traveler and is inconsistent with the rest of the question. What is really intended is not something we can fruitfully argue over; we should just hope that Kyle will edit the question to clarify the point. – whuber Feb 15 '15 at 16:53
  • 1
    @whuber, Ben is (somewhat backhandedly) pointing out a _typo_ not a logical or statistical fallacy. The asker wrote "...chance of dying in their next plane _crash_." which we all read as "...chance of dying on their next flight." – Shep Feb 15 '15 at 16:53
  • _"If you take a direct flight, you will be in the air, at risk of being in a crash, for 4 hours"_ - this assumes that the chance of death is per hour/minute/second of flight, not per takeoff or landing: you're looking at two separate probabilities here, and all you have is an averaged value. – Eric Feb 15 '15 at 21:28
  • What about the assumption of independence? Will weather, sleepy air traffic controllers, terrorist events, etc. alter the assumption of independence assumed? – StatsStudent Feb 15 '15 at 22:19
  • 2
    @BenVoigt I've revised my ambiguous language. I did not mean literally "the chance of dying in a plane crash." I actually meant, "the chance of getting into a place crash and then dying," exactly as whuber and Shep detected. Sorry for the confusion. – Kyle Feb 16 '15 at 08:56
  • 1
    @StatsStudent, the independence assumption absolutely doesn't hold for a frequent flyer. – Aksakal Feb 17 '15 at 14:08
  • The 1-in-10,000 chance being bandied about here is absolutely absurd. Your chances are more like 1-in-100million. You have 20x more chance of having a heart attack sat in a chair at home, than you do of being a fatality in an aviation accident – Jon Story Feb 17 '15 at 15:51
  • 1
    I don't think the root of this question is, really, a statistics one. You're debating whether the odds of dying in plane crash are primarily correlated with number of flights, or distance (the answer being both, but which is more). It's not a basic statistics question; it's a data analysis question. This is a question for [datascience.se], not CV. – Joe Feb 17 '15 at 23:04
  • It's actually far more effective to try and reduce the chance of being in a car accident. As we put people in tin cans together with fuel and propel them at extremely high speeds at extremely high heights, we're actually really careful in doing so. – Jasper Feb 19 '15 at 13:15
  • Regardless of numbers the probability of death after N flights can be approximated by 1 - (1-p)^N. p is the probability of death on a given flight. The probability that you do not die on N successive flights is P' = (1-p)^N. The probability that you die on one of them would be 1 - P'. This is not exact I think but reasonable. To be exact you would have to sum N terms where death occurs after k flights and you sum over k = 1 to N. – user3079275 Apr 20 '17 at 02:43

10 Answers10

61

Actual odds of planes crashing aside, you're falling into a logical trap here:

...each time one flies on an airplane, it does not increase the likelihood that he will die in a future airplane crash.

This is completely correct: whether you've never flown before or you've flown thousands of times, the chance of dying is still (in your example) 0.0001.

So if you're deciding between the two-hop and one-hop option, you're probably thinking about two scenarios:

  1. Future you, transferring between the two flights. Chance of dying on next flight: 0.0001.
  2. Future you, about to board the only flight. Chance of dying on next flight: 0.0001.

Same thing, right? Well, only if you assume you lived through the first flight in the first case. Put another way, in option 1, you're actually already dead 1/10,000th of the time.

The general issue is that you're confusing two scenarios:

  • your probability of being alive after $N$ flights
  • your probability of being alive after $N$ flights given that you were alive after $N-1$ flights.

Your chances of surviving one flight are always $1 - 0.0001$, but overall, the chances of living to the end of $N$ flights are $(1 - 0.0001)^N$

The Opposition View: I tried to keep my answer on topic by pointing out the logical issue rather than digressing into the empirical ones.

That said, in this case we may be letting the logic obscure the science. If your friend actually believes that skipping one flight will save him from a 1 in 10,000 chance of dying in a plane crash, the debate could be framed differently:

  • Your statement: a two-hop flight gives you a 0.0001 chance of dying
  • His statement: a two-hop flight gives a 0.0002 chance of dying

If this is the debate, it turns out that you are more correct. The actual odds of dying in a plane crash are about 1 in 2 million in the worst case. So you're both completely wrong, in that your estimates of airline fatalities are crazy high, but he's about twice as wrong as you are.

This 1 in 2 million figure is, of course, very rough and likely an overestimate. It's approximately correct to assume constant chances of dying per flight because (as many have pointed out) most accidents happen on takeoff and landing. If you really want the details, there's a lot more detail in another answer.

Condensed version: Your friend is right about probability theory, but given the statistics he's crazy to modify his behavior.

Community
  • 1
Shep
  • 810
  • 6
  • 10
  • 1
    Wow was I wrong. Thanks for explaining it out @Shep. Even though in the above scenario the difference is negligible, is paying the premium for a direct flight worth it not just for convenience, but for safety if you fly more than once a week? For a frequent flyer who flies for his job regularly, flying direct would significantly cut down on the chances of getting into a plane crash and dying, over the full span of his lifetime...right? – Kyle Feb 16 '15 at 08:48
  • 3
    The major flaw in this argument is an *assumption* that the probability of death in a flight is constant regardless of the nature and duration of the flight. In essence you're *assuming* that deaths are constant **per flight**. What makes you think it is true? This answer does not answer several OP's claims, particularly the claim that the deaths are constant **per mile**. So, the whole argument is speculative and actually wrong. As airline fatalities data show death rate is not constant **per flight**, e.g. commuter flights are more deathly than big airlines. – Aksakal Feb 16 '15 at 15:37
  • 8
    I think your statement that "you are more correct" is highly misleading: while the OP is closer to the real number, this is accidental; you're just saying that 0.0001 is closer to the real number than 0.0002. But it was just an example! The OP's **reasoning** is actually less correct than that of his friend who prefers a direct flight. – Roman Starkov Feb 16 '15 at 15:59
  • @romkyns this was in a second section for a reason. I said _if his friend actually believes the statistics he mentions_. My assumption was that it was just an example, but I didn't want people looking at this answer and saying "oh wow, I'd better cut down on the number of flights I take". – Shep Feb 16 '15 at 16:32
  • @kyle it depends on your definition of "significantly": if you fly once a week for the next 30 years you'll take about 1,500 trips. Given the (very rough, but generally worst-case) 1 in 2 million chances of dying in a plane crash, you could cut down your chances of dying in a plane crash by something like 1 in 1,000. A 1 in 1,000 risk is worth worrying about if you take it every day, but when that is the total risk in your lifetime it's really not worth worrying about. Your chances of dying in a car accident are 10 times higher. – Shep Feb 16 '15 at 16:51
  • @Kyle I should also add that you're probably not going to keep up one trip a week for the next 30 years... basically you should keep this in perspective: dying of fires, poisoning, being shot, or just _walking_ are all _individually_ more likely than air crashes _even if we assume you have a 1 in 1,000 chance of crashing_. (source: http://www.nsc.org/learn/safety-knowledge/Pages/injury-facts-chart.aspx) – Shep Feb 16 '15 at 16:54
  • @Aksakal, my aim with this answer was to _briefly_ explain the logical problems the OP was having. I added the rough statistics because I think probability theory is only as good as your data, but not a lot much because any science is only useful if people actually understand it. But I've also added a link to your answer (which is awesome, good work!). – Shep Feb 16 '15 at 17:09
  • @Aksakal I narrowed the best answers down to Shep's and yours. I ultimately chose Shep's because, while my "1 in 10,000" figure may be wrong, while my belief that most accidents occur while flying (as opposed to close to take-off/landing) may be wrong, and while I was wrong that longer flights produce more fatalities, these were auxiliary matters. I believe my fatal error was not looking at the _history_ of flights of a flyer, and instead just focusing on his _next_ flight. Shep addressed this error thoroughly and made me realize why my logic was wrong. – Kyle Feb 16 '15 at 19:35
  • @Kyle, consider this. Let's say you were right that accident rate is constant on *per mile* basis. So, it's like Poisson distribution with some $\lambda$ fatalities per 1000 miles. If you take one 2,000 miles flight, the expected death rate would be $2\lambda$. If you take two 1,000 mile flights, it's still $2\lambda$. Your *auxilliary* assumptions are not innocuous, as you see. If they were right, then your argument would have been valid. That's why it is important to go after the assumptions. They can change your conclusions to the opposite. These assumptions to be addressed only with data. – Aksakal Feb 16 '15 at 19:45
  • That said, I tend to agree that the addendum to Shep's answer, "The Opposition View" section, is somewhat confusing. Technically I suppose I was more correct, but the 1 in 10,000 figure was just a probability we threw out there as an example. The debate with my friend was never really about the numbers but about the logic. – Kyle Feb 16 '15 at 19:52
  • Some might say, "Well in this case, the numbers prove that the probability of dying is so low that it is illogical to modify your behavior." That opinion may be reasonable, but the fact remains that taking three planes to get to your destination instead of one _does increase the chances of dying due to a plane crash_ —however low that probability may be. – Kyle Feb 16 '15 at 19:52
  • @Kyle totally true. Also probably lowers your carbon footprint (if you care about such things). – Shep Feb 16 '15 at 20:20
  • @Aksakal you are absolutely correct and it _is_ important to go after all of my assumptions. I think your answer is really informative and provides relevant data. I simply believe the _most fallacious_ assumption I made was assuming that the total probability of death due to a crash for consecutive flights is equal to the probability of death due to a crash of the final flight. After all, it was this incorrect theoretical belief that the data-driven portion of my argument was predicated on. – Kyle Feb 16 '15 at 21:36
  • @Kyle, then maybe the best solution for the benefit of others is for you to leave only your main confusion in the question text, and for Shep to leave only the direct answer to this confusion. Because, as it is now Shep's answer has a few issues with unreasonable assumptions, yet in your words his answer somehow helped you to clear your confusion. – Aksakal Feb 17 '15 at 01:04
  • @Aksakal the question does have a few parts (maybe it would be nicer if it were more split up, maybe not) but I don't think editing the question now is really appropriate, especially if it changes the meaning of the question. See SO guidelines, which are explicitly against this http://stackoverflow.com/help/editing – Shep Feb 17 '15 at 01:32
  • To be really precise, if you would have a 0,0001 chance of dying every flight, you won't precisely have a 0,0002 chance of dying if you fly twice. In this case, that sounds a little bit counter intuitive, but compare it to a lottery: Imagine there's a lottery that gives you a 50% change of winning. This lottery is held every week. Imagine you take part in it in week 1 and in week 2, then with the same logic of two flight giving you a 0,0002 chance, this would mean you have a 100% chance of winning something and that is obviously not true. – Xander Feb 17 '15 at 11:07
  • The chance of having won something after week 2's lottery = the chance of winning something in week 1's lottery + the chance of losing in week 1's lottery * the chance of winning in week 2's lottery = 0,5 + 0,5*0,5 = 0,75. or from another point of view: the chance of having won something after week 2's lottery = 1 - the chance of not having won anything after week 2's lottery = 1 - (1-0,5)^2 = 0,75. – Xander Feb 17 '15 at 11:08
  • So if we apply this to the odds of dying in a plane crash, then chance of you having died in a plane crash after two flights = the chance of you dying in the first flight + the chance of you surviving the first flight * the chance of you dying in the second flight. Or again from a different point of view: the chance of you having died in a plane crash after n flights = 1 - the chance of you surviving n plane crashes = 1 - (1 - the chance of dying in a plane crash)^n. – Xander Feb 17 '15 at 11:08
  • So if we take 0,0001 as the chance of dying in a plane crash, that would mean the chance of you having died in a plane crash after 2 flight = 0,0001 + 0,9999*0,0001 = 0,00019999, so that's not a big difference with 0,0002. But now imagine you take 5.000 flights. Your intuition might say the chance of you dying in one of those flights = 5000 * 0,0001 = 0,5, but in reality, the chance of you dying in one of those flights = 1-(1-0,0001)^5000 = 0,393, so that's a lot less, so that does kinda favor you in the debate. – Xander Feb 17 '15 at 11:08
  • @Xander, In reality you are assuming independent and constant probability, which is not reasonable in this case. If you keep flying the same airline, the probabilities are obviously not independent. You are assuming the constant probability *per flight*, which is not reasonable. – Aksakal Feb 17 '15 at 14:15
  • 2
    @Xander, to answer your point, I know that the actual probability of dying on $N$ flights is $1 - (1-p)^n$, but when $p$ is a small number and $n$ isn't too large, this is approximately $np + \frac{1}{2} n(n-1)p^2 + O(p^3)$. I'm neglecting terms of $p^2$ or higher. – Shep Feb 17 '15 at 15:04
  • @Shep, you surely can neglect it in the case of n=2 and p=0.0001, but in reality you will take a lot more flights in a life time and then it doesn't necessarily have to be negligible. – Xander Feb 17 '15 at 21:22
  • @Xander, that's true, but in reality $p$ is closer to $10^{-6}$ and $n$ might be $10^{3}$. The first term $np$ will still be $10^{-3}$, the second will be roughly $10^{-6}$. In practice, as long as the first term remains "small" you can neglect the higher order terms. – Shep Feb 17 '15 at 21:28
39

Not only do you spend more time in-flight when you have two flights to your destination, even if the layover is collinear as the crow flies (since you will interrupt cruising speed), the greatest likelihood of accidents is in take-off and landing.

AdamO
  • 52,330
  • 5
  • 104
  • 209
  • 13
    +1 To labor the point a little ... taking two flights to get to a destination is nearly twice as risky as taking one. – Glen_b Feb 14 '15 at 23:55
  • Is there any evidence for this claim? Specifically, is there any evidence that the likelihood of _dying_ is highest on takeoff and landing? My impression is that this would not be the case. Fatailities I can think of are mid-flight incidents. MH370. MH17. Air Asia. Air NZ 901. Air France 447. Lockerbie. The list goes on. I can't name a single fatal commercial airliner indident that occured on takeoff/landing (I'm sure there are some, I'm just pointing out that it seems like there are less...) – GreenAsJade Feb 17 '15 at 02:36
  • 3
    @GreenAsJade: yes, quite a few, it varies greatly by year. [2013 was a particularly bad year for that with 10 out of 11 fatal accidents](http://en.wikipedia.org/wiki/List_of_accidents_and_incidents_involving_commercial_aircraft#2013) happening at or shortly before/after takeoff/landing/go-around. [2014 was very different, with only 2/9 such](http://en.wikipedia.org/wiki/List_of_accidents_and_incidents_involving_commercial_aircraft#2014) – smci Feb 17 '15 at 12:33
  • @smci Which is worse, take-off or landing? – Mitch Feb 17 '15 at 20:51
  • @Mitch: best to look at the stats, things vary. But frankly, airlines who rely on the autopilot are rumored to be the worst. Some airports have famously hard approaches (for landing), esp. in bad visibility. – smci Feb 18 '15 at 03:46
33

I'm going to answer all your questions. No, theory, all numbers.

My point was that each time one flies on an airplane, it does not increase the likelihood that he will die in a future airplane crash. That is, each airplane flight is independent. Whether someone has flown on 100 planes that year or just 1, both fliers still have a 1 in 10,000 chance of dying in their next plane crash.

This might be true as a standalone fact: independence of each crash occurrence. However, it's difficult to apply to a real life.

First, he probably meant to compare a frequent flyer vs. occasional flyer. If I fly a plane a couple of times a year to go to vacation, and his work involves weekly travel across the country, you must agree that he has a higher a chance of dying in a plane crash in the next year. We're not talking about one single flight, it's a lifestyle argument, or sample size in statistics.

Second, he's probably signed up to a frequent flyer program, which means that he always flies the same airline. Hence, the probability of a plane crash is probably more correlated in his case than in mine. So, the independence assumptions that you made is much weaker than it sounded first.

So, your friend is probably right.

Another point I made: say your destination is 4 hours away. If you take a direct flight, you will be in the air, at risk of being in a crash, for 4 hours. Now say you take 4 different connecting flights, each flight about an hour long. In this scenario you will still be in the air for roughly 4 hours. Thus, whether you take the direct flight or save some money and take connecting flights, the amount of time you spend at risk is roughly equal.

In 4 flights your cruising time is roughly the same as in 1 long flight, but you have 4 times more take-offs and descents. According to this web site, cruising is responsible for only 16% of fatalities. This graph shows the stats. You'll have more chance of dying in 4 short flights than in 1 long.

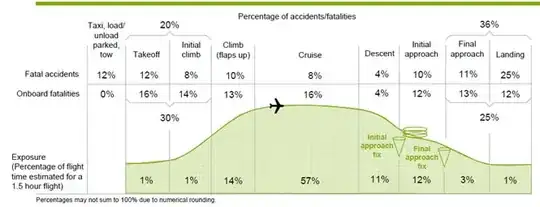
enter image description here

My final point was that shorter flights have a lower rate of crashes. I just pulled that one out of nowhere. I've done zero research and have zero data to back that up but...it seems logical.

This is probably not true. The shorter flights are more likely to be commuter flights, and these definitely have higher rates of fatalities according to this paper:

Throughout the period 1977–1994, scheduled commuter flights had far higher crash rates than major airlines

Here, you can find some stats too. Look at the table "Which type of flying is safer" rows with Part 135 vs. 121.

If you're taking shorter flights with major airlines (which is less likely), there's still an argument on per mile basis. Per mile, the shorter flight must have higher fatality because, as I showed earlier, because you need to takeoff and land more times per mile, and these phases are the most dangerous in terms of fatalities.

UPDATE: @AE question on what is not onboard fatalities. See this Boeing presentation with a ton of interesting data on airline crashes, where the airline accident is defined on p.3 as:

Airplane Accident: An occurrence associated with the operation of an airplane that takes place between the time any person boards the airplane with the intention of flight and such time as all such persons have disembarked

then the external fatalities are defined on p.4 as:

External fatalities include on-ground fatalities as well as fatalities on other aircraft involved.

The onboard means that death occurred to a passenger while he/she was onboard, see also CDC's reporting guideline here.

Aksakal
  • 55,939
  • 5
  • 90
  • 176
  • 3
    +1 Thank you, thank you for taking the answers out of the realm of speculation and using data to address the questions. – whuber Feb 15 '15 at 21:32
  • I like the graphic. One question about it though: Taxi (and load/unload etc) represents 12% of fatal accidents but 0% of onboard fatalities. Does that mean that the fatal taxiing accidents are fatal to persons not on-board the plane? Such as persons on the tarmac? I'm not sure I'm interpreting the graphic correctly... – A E Feb 16 '15 at 14:31
  • 1
    @AE, answered your question – Aksakal Feb 16 '15 at 15:23
  • Thanks @Aksakal! So does that mean that in an incident such as the [Tenerife airport disaster](http://en.wikipedia.org/wiki/Tenerife_airport_disaster) (a collision between KLM4805 and PanAm1736) the fatalities would be double-counted? I.e. that the passengers on KLM4805 would be counted once as 'on board' fatalities for KLM4805 and once as 'fatalities on other aircraft involved' for PanAm1736? I'm guessing that they wouldn't double-count but if fatal accidents for one aircraft include persons on-board another aircraft then I can't quite see how they'd work it. – A E Feb 16 '15 at 15:56
  • The pdf says "Airplane Collisions: Events involving two or more airplanes are counted as separate events, one for each airplane. For example, destruction of two airplanes in a collision is considered to be two separate accidents" so that does make it sounds like they double-count. – A E Feb 16 '15 at 15:58
  • @AE I don't know think they'd double count. I'm sure they take care of this in one way or another. – Aksakal Feb 16 '15 at 16:32
  • This is a great answer. I'm a bit confused by your logic around the frequent flyer program, though: I believe that some airlines are safer than others, but since you're pulling the "all data" angle, I think you need stats to back that up. – Shep Feb 16 '15 at 17:13
  • @Shep, frequent flyer program argument goes against the *independence* assumption. OP claims that the probability of death in the next flight does not depend on your flight history. I'm saying that this claim is not obviously correct because of the existence of frequent flyer programs. If you always fly the same airline, it's hard to claim that you have the same probability of death as someone who picks airlines randomly, because there's a reasonable argument for correlation. So, OP has to back his independence argument with data. – Aksakal Feb 16 '15 at 17:20
  • there's a reasonable argument, sure, but the fact remains that crashes are _very_ random, and picking out individual airlines lowers your sample size and opens the door for multiple hypothesis testing biases. Is it reasonable to say that Malaysian Airlines is unsafe because they were responsible for most of the deaths last year? I wouldn't assume so without seeing a rigorous statistical analysis (I've generally heard they had a very good safety record). Sorry, I'm not trying to say this is a bad answer, just that that section is a bit of conjecture in an otherwise flawless answer. – Shep Feb 16 '15 at 17:26
  • I've opened another question about this: http://stats.stackexchange.com/questions/137939/is-there-a-statistically-valid-ranking-for-safe-international-airlines – Shep Feb 16 '15 at 17:46
  • @Shep, is it reasonable to assume that Malasian Airlines is as safe as other airlines? I don't think so, anymore. In statistics you test the restrictions, not the absence of them. In this case you set a restriction when you say all airlines are equally safe. It's a strong assumption, which must be somehow supported by facts. – Aksakal Feb 16 '15 at 18:20
  • @Aksakal, I didn't say that all airlines are equally safe at all. I was just thrown off by this sentence "Hence, the probability of a plane crash is probably more correlated in his case than in mine. So, the independence assumptions that you made is much weaker than it sounded first." It's just very unclear what you're saying here; you invoke _three_ people, then somehow misconstrue the OPs independence argument as something that relies on flying different airlines (crashing is independent of past flights even on one airline). The rest of the answer is very nice, this part is just confusing. – Shep Feb 17 '15 at 00:45
  • @Shep, "crashing is independent of past flights even on one airline" - this is not the claim that you have to prove. You're making an independence assumption. The independence assumptions are notoriously difficult to prove, especially on such low count data as airline crashes. I'll argue that each airlines has its own safety process, and implements it in own way in terms training, audit, checks etc. Hence, it's reasonable to doubt your independence claim. It's on you to prove it, not on me to doubt it. – Aksakal Feb 17 '15 at 00:59
  • @Aksakal, I didn't say crashing was independent of airline, just that its dependence on airline _isn't relevant_ to the OP's question. The OP stated that the chances of crashing on a given flight were independent of _how many flights he had taken in the past_. This is a completely reasonable assumption. His problem was failing to compound probabilities, not independence assumptions. – Shep Feb 17 '15 at 01:15
14

He stated that he prefers to fly direct to a destination, as it decreases the probability that he will die in an airplane crash.

If your friend is genuinely concerned about this incredibly low probability then they should not be flying at all, or, for that matter, driving to the airport.

His logic was that if the probability of a commercial airline crash is 1 in 10,000, flying on two planes to get to your destination would double your chance of death.

This is correct. I propose a game. Here are your choices:

Option 1 You flip a coin. Heads I win, tails, you win.

Option 2 You flip a coin. Heads I win, tails, you flip the coin again, heads, I win, tails, you win.

Me "winning" is you dying in a plane crash, you "winning" is you survive. Option 1 is you taking a single flight, option 2 is you attempting to take two flights, but you might only end up taking one if the first one crashes.

Are the two options the same in terms of their likely outcomes, or different? Which would you pick if I gave you this game? If we were betting money on it, what would be fair odds for me to give you?

My point was that each time one flies on an airplane, it does not increase the likelihood that he will die in a future airplane crash.

Correct. Each time you fly it decreases the likelihood that you will die in a future crash because you might die in the current flight, and so there will be no future flight to die in!

That is, each airplane flight is independent. Whether someone has flown on 100 planes that year or just 1, both fliers still have a 1 in 10,000 chance of dying in their next plane crash.

Sure, but you had to survive those 100 flights.

In my game, suppose you choose option two. You flip tails. You are saying "the next one is still 50-50", but you should be saying "if I'd chosen option 1 and flipped that tails, I'd be safe now, instead of once again in danger of flipping heads". When you get off that plane having lived, you lived. Had you gotten off dead, you wouldn't be at any risk of dying on the following flight.

If you take a direct flight, you will be in the air, at risk of being in a crash, for 4 hours. Now say you take 4 different connecting flights, each flight about an hour long. In this scenario you will still be in the air for roughly 4 hours. Thus, whether you take the direct flight or save some money and take connecting flights, the amount of time you spend at risk is roughly equal.

No, that is empirically false. The vast majority of fatal commercial air disasters occur at takeoff or landing, and there is one of those per leg. Being in the air for four hours is only slightly more risky than being in the air for one, but four takeoffs are much riskier than one takeoff.

Eric Lippert
  • 409
  • 2
  • 6
5

Simple answer. You are correct in assuming the probability is the same for each flight, but when you make a connection you're effectively "rolling the dice" again.

Furthermore, it's commonly known that the most dangerous points of any flight are take off and landing—thus taking a connection exposes yourself to these risks a second time.

Peter
  • 151
  • 2
4

Your friend is right (on the probability theoretical side, not in in practice).

Apply your logic to throwing dice: you are saying that the chances of not throwing snake eyes once in 100 throws (i.e. surviving 100 flights) are the same as those of not throwing snake eyes in one throw (i.e. surviving one flight). If you really think that, then I'm really interested in playing dice with you.

jscs
  • 103
  • 3
Martin Argerami
  • 141
  • 3
2

Your chances of a coin flip coming up heads or tails are 50/50, on EVERY flip.

However, it is highly unlikely you would ever get a run of 10 heads in a row.

A little mathematics can be a dangerous thing :-)

Laurence Payne
  • 139
  • 2
  • 6
    How is this point relevant to the question? – whuber Feb 15 '15 at 16:21
  • By analogy, @whuber: if "tails" represents "dies in a plane crash", then the mechanics here are the same as those in the question, although the numerical value is different. Just replace the answer's fair coin with one that's rigged to come up heads 9,999 times out of 10,000. – jscs Feb 15 '15 at 19:58
  • And what is "a run of 10 heads in a row" analogous to? Are you trying to claim that it would be unusual to live through ten airplane flights?? When you want to use an analogy, don't be coy about it: explain how the analogy works and apply it explicitly, lest people misunderstand you. – whuber Feb 15 '15 at 21:31
  • I have to agree; it's only a good answer if you already know what's wrong with the question-asker's logic. – Peter Cordes Feb 16 '15 at 07:01
  • Using a fair coin to illustrate a binomial distribution is much less applicable here than you would think. Even assuming the anecdotal "1/10,000" aggregate risk statistic, dying from a plane crash is not a fair exercise. "Chance of dying on a properly maintained aircraft" vs "chance of dying on an AirAsia aircraft" ...not the same. – K. Alan Bates Feb 17 '15 at 16:21
2

An intuitive way of looking at this, in my opinion, is the concept of micromort (one-in-a-million probability of death).

According to Wikipedia, you'll 'accumulate' roughly one micromort due to accidents for each 1000 miles traveled and roughly one micromort due to terrorism for every 12'000 miles (in the U.S.).

This implicitly assumes that the probability of a fatal incident is proportional to the number of miles flown, independent of the number of takeoffs and landings. You'll likely get an opinion on how justified this is on https://aviation.stackexchange.com/ .

Community
  • 1
Andre Holzner
  • 1,103
  • 2
  • 9
  • 17
  • Counter-intuitively, with this simplification you arrive at a conclusion that describes an average case that does not exist. Due to the distributions pointed out by others, the micromorts you suffer on a short flight accrue way faster than 1 in 1000 miles and for longer flights, way way less. – John Shedletsky Feb 19 '15 at 09:05
2

I believe that you and your friend have missed one important variable. That is are the chances of dying in a plane crash disproportionately concentrated in the takeoff and landing. Off the top of my head, I believe the answer is yes.

Your friend's argument is, if you fly direct for 1000 miles, versus flying two flights for 500 miles each, you've flown the same 1000 miles in each case, and therefore your chances of dying are comparable.

Your version (of my argument) would be something like "if you fly direct, you've taken off and landed once, whereas the other way, you've taken off and landed twice." If my premise (about take off and landing) is correct, the second way is almost twice as dangerous as the first. And even if my premise is wrong, that's the question you should ask.

Tom Au
  • 181
  • 1
  • 7
1

You have to ask yourself what this “probability of dying in plane crash” represents and how it applies to your problem (or not).

Look at it this way:

  • If you never fly at all, your chances to die in a plane crash are going to be much lower (but not nil, cf. El Al Flight 1862 or Air France Flight 4590).
  • If you fly every day for most of your life, your chances to die in a plane crash are obviously higher than if you don't.

It seems to me that there is plausible model of how plane crash deaths happen that make them completely unrelated to being in an airplane.

Consequently, I would guess that this 1 in 10,000 figure does not quite mean what you think it means. Maybe it's an average based on comparing deaths in plane crash to other causes of death or it's a reasonable estimate of the risk based on a typical “flying profile” in your country but it can't possibly be exactly the same for people with widely different plane-taking behaviour.

The difference between one flight and two flights might be tiny and your scenario also invites thinking about the difference between one flight (one take-off/one landing) and time spent in the air but if you do accept that people who never fly have a lower risk of dying in a plane crash than people who fly constantly, you can't assume than the probably of dying in a plane crash in completely independent from the number of flights you take.

Gala
  • 8,323
  • 2
  • 28
  • 42