I'm following along here: http://reliawiki.org/index.php/Multiple_Linear_Regression_Analysis#Calculation_of_the_Statistic
I've successfully made all of the calculations up to $f_0=211.9$. Now I need to calculate $f_{\alpha, k, n-(k+1)}$. On the page, this is simply given as:
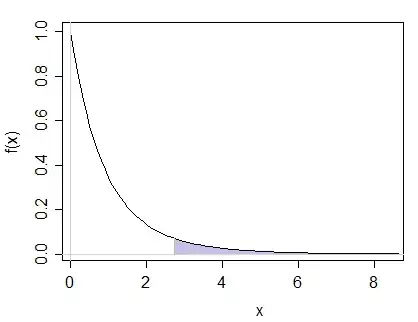
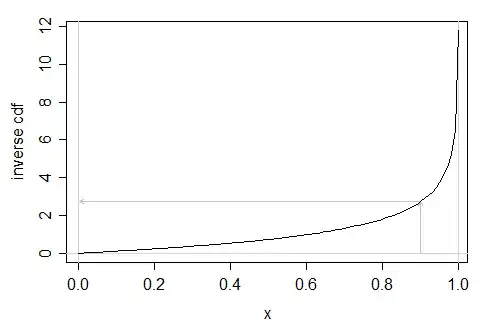
The critical value for this test, corresponding to a significance level of 0.1, is:
$$f_{\alpha, k, n-(k+1)} = f_{0.1, 2, 14} = 2.726$$
I understand that $n$ is the number of observations and $k$ is the degrees of freedom. But, how is this number, $2.726$, calculated?
[[Edit: more questions]]
Is this value the result of the CDF for the F-distribution?:
$$F(x; d_1, d_2) = I_{\frac{d_1x}{d_1x+d_2}}(\frac{d_1}{2}, \frac{d_2}{2})$$
Where $x$ is $0.1$, $d_1$ is $2$ an $d_2$ is $14$? and $I$ is:
$$I_v(a,b) = \frac{B(v; a, b)}{B(a, b)}$$
And $B$ is:
$$B(v; a, b) = \int_{0}^{v}t^{a-1}(1-t)^{b-1}dt$$
and
$$B(a, b) = \int_{0}^{1}t^{a-1}(1-t)^{b-1}dt$$