1

First off, I don't know a lot of stats. That said, I am hoping you can help me derive the function to calculate the fitted probability from the summary of a logistic regression below:

enter image description here

My instinct is that the formula would be...

$$ P= 1/(1+e^{-z}) $$ Where

$z= B_0 + x_1B_1 + x_2B_2 + ... + X_pB_p$

where

$B_1 = ln(OR)$

However, the results I am getting from this formula do not seem to be correct. Here's why I think it is wrong or that I am making a mistake:

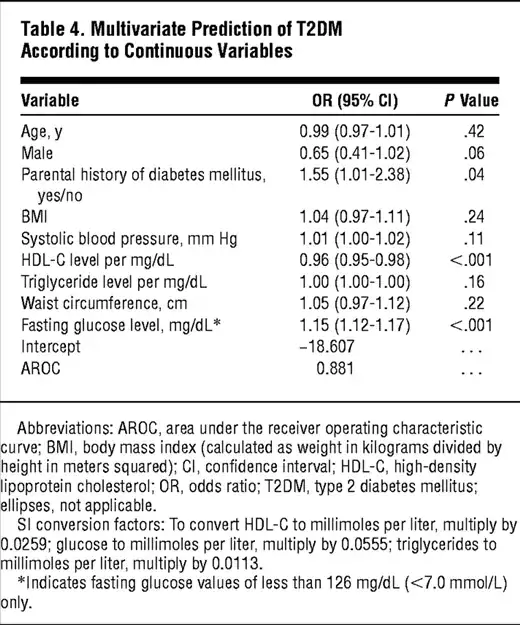
When I model the formula as written in my question above,

  • I am getting an inverse correlation between age and diabetes risk, which is counter intuitive.
  • When I compare the results between the continuous model (Table 4) and the model with discreet variables (Table 3), the results are pretty different.
  • The only variable that seems to matter in the continuous model is fasting blood glucose. I know this is a strong indicator for diabetes, but what's the point of having the other variables if they barely affect the probability.

For example, from my model, I get the following results:

Example

Gender: Male Age: 34 BP: 145/95 BMI: 38.5 Waist Circ: 42 HDL-C: 45 Triglycerides: 100 Fasting glucose: 85 Diabetes History: N

I get the following results:

  • (p) = 2.6% in discreet model (table 3)
  • (p) = 23.5% in continuous model (table 4)

If I hold all the variables constant and only change the age from 34 to 45, I get the following results:

  • In discreet model, (p) remains the same at 2.6%. This makes sense given that age is categorical.
  • In continuous model, (p) = 18.5%

I am surprised that the probability is declining as we increase the age. Based on intuition and knowledge of the progression of diabetes, I would expect the opposite.

Am I doing something wrong?

The full study I am referencing is: http://archinte.jamanetwork.com/article.aspx?articleid=486842#ioi70028t4

If anyone could help me derive the probability of diabetes from this study using the continuous variable model, I would be very grateful!

Thank you in advance for your help.

Jon Cooper
  • 11
  • 3
  • I think this is fully explained at http://stats.stackexchange.com/questions/133623. Is my answer there overlooking something you need? Could you show an example of your calculation and tell us why you think it is incorrect? – whuber Feb 11 '15 at 22:38
  • Thank you for the link to the great response. @Glen_b - thank you for cleaning up my question. Here's why I think there is an error in my calculation. When I model the formula as written in my question above, I am getting an inverse correlation between age and diabetes risk, which is counter intuitive. Also, when I compare the results between the continuous model (Table 4) and the model with discreet variables (Table 3), the results are pretty different. In fact, the only variable that seems to matter in the continuous model is fasting blood glucose. Am I doing something wrong? – Jon Cooper Feb 12 '15 at 19:12
  • Jon - Actually, most of that cleanup was done by [AndrewM](http://stats.stackexchange.com/revisions/137322/2); I just tweaked it a tiny bit when the edit came up for review (edits get checked until you've been doing it a while). There should be a red "edited ... ago" link above my gravatar/name under your post, if you click it you can follow the edit history. When it came up for review, I selected the option to improve the suggested edit and made an additional change. If you don't like an edit, you can always change it/roll it back (though they're normally done for a good reason). – Glen_b Feb 12 '15 at 23:28
  • Jon, that reasoning why you think the answer might be wrong should also be edited into your question (so later readers don't have to scan the comments to find out what you think the problem is). – Glen_b Feb 12 '15 at 23:34
  • @whuber - please pardon my ignorance. I read the link you posted and think, but am still uncertain, that I am indeed converting between the OR and regression coefficients correctly, and thus my expanded examples would be correct. Would you mind confirming that? If so, should I just attribute the inverse relationship between age and diabetes risk as a statistical quirk and attribute that to the high p value? If so, dare I ask why the study authors would even include the age as a variable in the model? Sorry for the stat novice questions. PS: good to see a fellow Philadelphian! – Jon Cooper Feb 18 '15 at 19:45

0 Answers0