Compare two binomials with unequal groups of trials

Question

I'm attempting to determine if store B is 'better' than store A. Let's say that the two stores are identical in every way except for the sales assistants. I'd like to determine if one store makes more money than the other.

The problem is a dearth of data. On any given day, for each store, I get the number of people who entered the store and the dollar amount purchased. That's it. The dollar amount purchased could represent multiple sales or a single purchase; I can't know the difference. Here is some data:

Day customers sales customers sales
Day 1   7    $-    9  $-   
Day 2   25   $-    5  $-   
Day 3   14   $-    13  $-   
Day 4   8    $-    12  $-   
Day 5   6    $-    17  $-   
Day 6   20   $-    29  $-   
Day 7   7    $-    27  $-   
Day 8   30   $-    71  $-   
Day 9   91   $-    141  $8.88 
Day 10  30   $-    20  $-   
Day 11  29   $-    10  $-   
Day 12  136  $-    80  $-   
Day 13  99   $3.96  132  $4.50 
Day 14  116  $-    73  $-   
Day 15  65   $17.84  60  $-   
Day 16  95   $-    150  $-   
Day 17  82   $-    115  $5.07 
Day 18  172  $-    70  $1.88 
Day 19  101  $5.21  195  $-   
Day 20  190  $-    148  $-   
Day 21  130  $-    162  $37.89 
Day 22  92   $1.03  154  $4.01 
Day 23  123  $-    97  $-   
Day 24  158  $-    112  $-   
Day 25  109  $-    128  $1.96 
Day 26  206  $-    140  $-   
Day 27  132  $-    134  $0.16 
Day 28  180  $-    143  $1.77 
Day 29  155  $-    129  $4.99 
Day 30  80   $-    128  $5.86 
Day 31  214  $-    156  $0.50 
Day 32  392  $1.75  261  $-   
Day 33  201  $-    132  $-   
Day 34  225  $-    148  $3.24 
Day 35  145  $-    204  $-   
Day 36  126  $-    105  $

The 2nd and 3rd columns are customers and sales in Store A and the 4th and 5th columns are customers and sales in Store B.

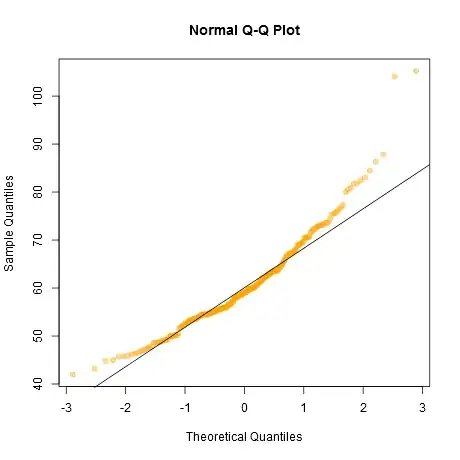
The earnings are not normally distributed, so I can't run a t-test. With a lot more data perhaps they would become normally distributed, or I could take averages of a much greater data set, but this is the data that I have to work with right now.

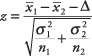
Store B, however, appears to have a much greater incidence of non-zero values, which is a binomial distribution, so perhaps I could show % of non-zero sales values. Store A produced sales 14% of the days and store B produced sales 36% of the days. Following Test if two binomial distributions are statistically different from each other I could calculate the test statistic and compare it to the critical region value, but unfortunately each day does not have the same number of customers. Basically I don't have the result of every individual trial (a customer enters a store) and the trails are irregularly grouped.

So how would I go about showing significance here?

Answer 1

If I were a store owner I would primarily be concerned about total sales.

Sales would likely vary with date: on a holiday or weekend, for instance, sales might go down (or up!) systematically. To account for such common components of variability, we may compare store sales day by day.

Sales clearly are erratic, so we should be cautious about applying methods that make strong distributional assumptions or rely on asymptotic results.

These considerations suggest applying a permutation test. The null hypothesis--which we should accept in the absence of evidence to the contrary--is that both stores are equally effective in generating sales. Under this null hypothesis, the sales amounts generated by the two stores on any particular day are exchangeable: they could have occurred at either store. We are interested in whether the observed amounts could be explained by such chance differences.

Accordingly, we could create all $2^{36}$ possible datasets derivable from this one by means of switching the sales figures for all possible subsets of the days. In each such "synthetic" dataset we would like to measure the differences in sales performance. One natural way is to compute the (absolute) difference in total sales. The resulting set of $2^{36}$ numbers is the permutation distribution of the total sales difference. If the observed total sales difference is an extremely large member of this distribution, we would reject the null hypothesis. The correct measurement of "extremely large" is the fraction of the permutation distribution consisting of equal or larger differences: it is the "p-value."

Doing these 70 billion or so calculations is possible but time-consuming. Once the dataset grows by a few more days, the approach would be impracticable. Instead, we may sample from the permutation distribution in order to approximate it. Because the distribution contains so many results, we may sample "with replacement" -- in other words, we don't really need to track whether a particular sample shows up multiple times in our work, because this will be a rare event and will not appreciably affect the approximation. This results in an extremely fast procedure, allowing us easily to generate $10^5$, $10^6$, or more cases within a second. For these data, $10^5$ iterations will estimate the true permutation test p-value to almost three decimal places, which is more than good enough. It turns out (as shown below) to equal $0.317$. That number is so large that it would be unreasonable to suggest that the observed differences are due to anything other than chance.

Histogram of a sample (of size 100,000) from the permutation distribution. The solid orange bars represent values equal to or exceeding the observed difference of 50.92. They comprise 31.7% of the sample. (The final digit "7" is uncertain due to use of a sample of the permutation distribution to estimate the p-value.)

The R code to compute this permutation distribution follows.

sales <- cbind(A=c(rep(0, 12), 396,0,1784,0,0,0,521,0,0,103, rep(0,9),175,rep(0,4)),
               B=c(rep(0, 8), 888, 0,0,0, 450, 0,0,0, 507, 188, 0,0, 3789,
                 401, 0,0,196,0,16,177,499,586,50,0,0,324,0,0))/100

sales.stat <- abs(sum(sales[, "A"]) - sum(sales[, "B"]))
n <- dim(sales)[1]
n.iter <- 1e5
sim <- replicate(n.iter, sum(sales[cbind(1:n, 1+floor(runif(n)*2))]))
sim <- abs(2*sim - sum(sales))
sim <- c(sales.stat, sim)
p.value <- sum(sim >= sales.stat) / length(sim)

Answer 2

This question is getting no love, so I'm going to take a crack at it. I don't know if this is the right answer of not, so perhaps someone can help with that.

Using the daily success rate as a binomial appears to be problematic since each store doesn't have the same number of customers on any given day. Throughout the period of the experiment there are approximately the same number of customers in each store, but they aren't uniformly distributed and I'm not sure how to smooth out the data to account for this.

Therefore, I'm back to looking at a straightforward 2-sample z-test using sales.

Since again I don't have the data for each customer, and each store has a different number of customers on each day, I decided to 'normalize' using sales per 100 customers. As such:

delta = zero
n = number of customers during the experiment / 100
x = sales per 100 customers = sales / n

Sigma is problematic since, again, I don't have individual customer sales data and on any given day the number of customers in each store varies. To resolve this, to get a collection of sales per 100 customers data points I took the sales on each day and scaled it by the number of customers that were in each store on that day. Simply put, for each store on each day it's sales / number of customers * 100. (The data is below and it's frankly terrible how there seems to be no good way to post it here, but you can copy/paste to Excel.)

Solving for the values I get this:

Store A
n = 39.91
x = $0.75
sigma = $4.65

Store B
n = 37.10
x = $2.12
sigma = $4.10

z = (2.12 - 0.75)/sqrt( (4.65^2 / 39.91) + (4.10^2 / 37.10) ) = 1.43

A z of 1.43 give me a standard normal cumulative distribution of 0.92. The two-tail alpha is thus 0.15 for 85% confidence.

How does this look?

,customers,sales,sales/100 customers,customers,sales,sales/100 customers
Day 1,7, $-   , $-   ,9, $-   , $-   
Day 2,25, $-   , $-   ,5, $-   , $-   
Day 3,14, $-   , $-   ,13, $-   , $-   
Day 4,8, $-   , $-   ,12, $-   , $-   
Day 5,6, $-   , $-   ,17, $-   , $-   
Day 6,20, $-   , $-   ,29, $-   , $-   
Day 7,7, $-   , $-   ,27, $-   , $-   
Day 8,30, $-   , $-   ,71, $-   , $-   
Day 9,91, $-   , $-   ,141, $8.88 , $6.30 
Day 10,30, $-   , $-   ,20, $-   , $-   
Day 11,29, $-   , $-   ,10, $-   , $-   
Day 12,136, $-   , $-   ,80, $-   , $-   
Day 13,99, $3.96 , $4.00 ,132, $4.50 , $3.41 
Day 14,116, $-   , $-   ,73, $-   , $-   
Day 15,65, $17.84 , $27.45 ,60, $-   , $-   
Day 16,95, $-   , $-   ,150, $-   , $-   
Day 17,82, $-   , $-   ,115, $5.07 , $4.41 
Day 18,172, $-   , $-   ,70, $1.88 , $2.69 
Day 19,101, $5.21 , $5.16 ,195, $-   , $-   
Day 20,190, $-   , $-   ,148, $-   , $-   
Day 21,130, $-   , $-   ,162, $37.89 , $23.39 
Day 22,92, $1.03 , $1.12 ,154, $4.01 , $2.60 
Day 23,123, $-   , $-   ,97, $-   , $-   
Day 24,158, $-   , $-   ,112, $-   , $-   
Day 25,109, $-   , $-   ,128, $1.96 , $1.53 
Day 26,206, $-   , $-   ,140, $-   , $-   
Day 27,132, $-   , $-   ,134, $0.16 , $0.12 
Day 28,180, $-   , $-   ,143, $1.77 , $1.24 
Day 29,155, $-   , $-   ,129, $4.99 , $3.87 
Day 30,80, $-   , $-   ,128, $5.86 , $4.58 
Day 31,214, $-   , $-   ,156, $0.50 , $0.32 
Day 32,392, $1.75 , $0.45 ,261, $-   , $-   
Day 33,201, $-   , $-   ,132, $-   , $-   
Day 34,225, $-   , $-   ,148, $3.24 , $2.19 
Day 35,145, $-   , $-   ,204, $-   , $-   
Day 36,126, $-   , $-   ,105, $-   , $-   
Total,3991, $29.79 , $38.17 ,3710, $80.71 , $56.64