Does 10 heads in a row increase the chance of the next toss being a tail?

Question

I assume the following is true: assuming a fair coin, getting 10 heads in a row whilst tossing a coin does not increase the chance of the next coin toss being a tail, no matter what amount of probability and/or statistical jargon is tossed around (excuse the puns).

Assuming that is the case, my question is this: how the hell do I convince someone that is the case?

They are smart and educated but seem determined not to consider that I might be in the right on this (argument).

Answer 1

they are trying to assert that [...] if there have been 10 heads, then the next in the sequence will more likely be a tail because statistics says it will balance out in the end

There's only a "balancing out" in a very particular sense.

If it's a fair coin, then it's still 50-50 at every toss. The coin cannot know its past. It cannot know there was an excess of heads. It cannot compensate for its past. Ever. it just goes on randomly being heads or tails with constant chance of a head.

If $n_H$ is the number of heads in $n=n_H+n_T$ tosses ($n_T$ is the number of tails), for a fair coin, $n_H/n_T$ will tend to 1, as $n_H+n_T$ goes to infinity .... but $|n_H-n_T|$ doesn't go to 0. In fact, it also goes to infinity!

That is, nothing acts to make them more even. The counts don't tend toward "balancing out". On average, imbalance between the count of heads and tails actually grows!

Here's the result of 100 sets of 1000 tosses, with the grey traces showing the difference in number of head minus number of tails at every step.

The grey traces (representing $n_H-n_T$) are a Bernoulli random walk. If you think of a particle moving up or down the y-axis by a unit step (randomly with equal probability) at each time-step, then the distribution of the position of the particle will 'diffuse' away from 0 over time. It still has 0 expected value, but its expected distance from 0 grows as the square root of the number of time steps. [Note for anyone thinking "is he talking about expected absolute difference or the RMS difference" -- actually either: for large $n$ the first is $\sqrt{2/\pi}\approx$ 80% of the second.]

The blue curve above is at $\pm \sqrt{n}$ and the green curve is at $\pm 2\sqrt{n}$. As you see, the typical distance between total heads and total tails grows. If there was anything acting to 'restore to equality' - to 'make up for' deviations from equality - they wouldn't tend to typically grow further apart like that. (It's not hard to show this algebraically, but I doubt that would convince your friend. The critical part is that the variance of a sum of independent random variables is the sum of the variances $<$see the end of the linked section$>$ -- every time you add another coin flip, you add a constant amount onto the variance of the sum... so variance must grow proportionally with $n$. Consequently the standard deviation increases with $\sqrt{n}$. The constant that gets added to variance at each step in this case happens to be 1, but that's not crucial to the argument.)

Equivalently, $\frac{|n_H-n_T|}{n_H+n_T}$ does go to $0$ as the total tosses goes to infinity, but only because $n_H+n_T$ goes to infinity a lot faster than $|n_H-n_T|$ does.

That means if we divide that cumulative count by $n$ at each step, it curves in -- the typical absolute difference in count is of the order of $\sqrt{n}$, but the typical absolute difference in proportion must then be of the order of $1/\sqrt{n}$.

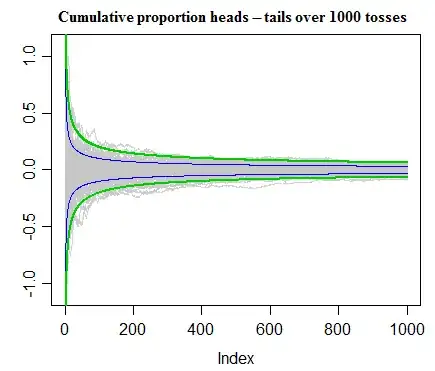
That's all that's going on. The increasingly-large* random deviations from equality are just "washed out" by the even bigger denominator.

* increasing in typical absolute size

See the little animation in the margin, here

If your friend is unconvinced, toss some coins. Every time you get say three heads in a row, get him or her to nominate a probability for a head on the next toss (that's less than 50%) that he thinks must be fair by his reasoning. Ask for them to give you the corresponding odds (that is, he or she must be willing to pay a bit more than 1:1 if you bet on heads, since they insist that tails is more likely). It's best if it's set up as a lot of bets each for a small amount of money. (Don't be surprised if there's some excuse as to why they can't take up their half of the bet -- but it does at least seem to dramatically reduce the vehemence with which the position is held.)

[However, all this discussion is predicated on the coin being fair. If the coin wasn't fair (50-50), then a different version of the discussion - based around deviations from the expected proportion-difference would be required. Having 10 heads in 10 tosses might make you suspicious of the assumption of p=0.5. A well tossed coin should be close to fair - weighted or not - but in fact still exhibit small but exploitable bias, especially if the person exploiting it is someone like Persi Diaconis. Spun coins on the other hand, may be quite susceptible to bias due to more weight on one face.]

Answer 2

The confusion is because he is looking at the probability from the start without looking at what else has already happened.

Lets simplify things:

First flip:

T

Now the chance of a T was 50%, so 0.5.

The chance that the next flip will be T again is 0.5

TT 0.5
TF 0.5

However, what about the first flip? If we include that then:

TT 0.25
TF 0.25

The remaining 50% is starting with F, and again has an even split between T and F.

To extend this out to ten tails in a row - the probability that you already got that is 1/1024.

The probability that the next one is T or F is 50%.

So the chance from the start of 11 tails is 1 in 2048. The probability that having already flipped tail 10 times that the next flip will also be a tail though is still 50%.

They are trying to apply the unlikeliness of the 1 in 1024 odds of 10 T to the chance of another T, when in fact that has already happened so the probability of it happening is no longer important.

11 tails in a row are no more or less likely than 10 tails followed by one head.

The probability that 11 flips are all tails is unlikely but since it has already happened it doesn't matter any more!

Answer 3

The odds are still 50-50 that the next flip will be tails.

Very simple explanation: The odds of flipping 10 heads + 1 tail in that order are very low. But by the time you've flipped 10 heads, you've already beaten most of the odds... you have a 50-50 chance of finishing the sequence with the next coin flip.

Answer 4

You should try convincing them that if the previous results were to impact the upcoming tosses then not only the last 10 tosses should have been taken into consideration, but also every previous toss in the coin life.

I think it's a more logical approach.

Answer 5

To add to earlier answers, there are two issues here, first, what happens when the count is actually fair and each toss is independent of all other tosses. Then, we have the "law of large numbers", saying that in the limit of an ever increasing sequence of tosses, the frequency of tails will approach probability of tail, that is, $1/2$.

If the first ten tosses all were tails, then the limiting frequency will still be one half, without any need of later tosses "balancing out" the first ten tails! Algebraically , let $x_n$ be the number of tails among the throws $11, 12, \dots, n+10.$. Lets assume that actually we get $$ \lim_{n \rightarrow \infty} x_n/n =1/2 $$ Then when taking into account the first ten tosses, we will still have the limit $$ \lim_{n \rightarrow \infty} \frac{10+x_n}{n+10}= 1/2 $$ That is, after one million and ten tosses, we have that $$ \frac{10+500000}{1000010} \approx 0.5 $$ so, in the limit, the first 10 tails doesn't matter at all, its effect is "washed out" by all the later tosses. So, there is no need of "balancing out" for the limit result to hold. Mathematically, this is just using the fact that the limit (if exists ...) of any sequence of numbers do not depend at all on any finite, initial segment! So we can arbitrarily assign the results for the first ten (or first hundred) tosses without affecting the limit, at all. I guess this way of explaining it to your gambler friends (maybe with more numbers & examples and less algebra ...) might be the best way.

The other aspect is: After ten tosses ten tails, maybe somebody starts to doubt if the coin is a good one, corresponds to the simple, ordinary model of independent, equal probability tosses. Assuming the "tosser" (the person doing the tossing) haven't been trained to control the tosses in some way, and is really tossing in a honest way, the probability of tail must be one half (see this Gelman paper.)

So then there must be, in the alternative hypothesis, some dependence among the coin tosses! And, after seeing ten tails in a row, the evidence is that the dependence is a positive one, so that one tail increases the probability that the next coin toss will be tail. But then, after that analysis, the reasonable conclusion is that the probability of the eleventh toss being a tail, is increased, not lowered! So the conclusion, in that case, is the opposite of your gamblers friends.

I think you will need a very strange indeed model to justify their conclusions.

Answer 6

This isn't really an answer - your problem is psychological, not mathematical. But it may help.

I often face your "how the hell ..." question. The answers here - mostly correct, are too mathematical for the people you're addressing. One place I start is to try to convince them that flipping one coin 10 times is essentially the same as flipping 10 coins simultaneously. They can grasp the fact that sometimes you'll see 10 heads. In fact that happens about once in a thousand tries (since $2^{10} \approx 10^3$). If 15,000 people try this then about 30 of them will think they have special coins - either all heads or all tails. If they accept this argument then the step to sequential tosses is a little easier.

Answer 7

Assuming coin flips are independent, this is very easy to prove from one statistician to another. However, your friend seems to not believe that coin flips are independent. Other than throwing around words that are synonymous with independent (for example, the coin doesn't have a "memory") you can't prove to him that coin flips are independent with a mere word argument. I would suggest using simulation to assert your claim but, to be honest, if your friend doesn't believe coin flips are independent I'm not sure he'll believe simulation results.

Answer 8

To restate some of the explanations already given (by @TimB and @James K), once you've flipped a coin 10 times and got 10 heads, the probability of getting 10 heads in a row is exactly 1.0! It's already happened, so the probability of that happening is now fixed.

When you multiply that by the probability of getting heads on your next flip (0.5), you get exactly 0.5.

Betting on tails with anything other than even odds at that point is a sucker's bet.

Answer 9

Let's say I'm convinced that the coin is fair. If the coin was fair then the probability of having 10 heads in a row is $$p_{10}=\left(\frac{1}{2}\right)^{10}=\frac{1}{1024}<0.1\%$$ So, as a frequentist at $\alpha=1\%$ significance, I must reject the $H_0$:coin is fair, and conclude that the $H_a$: "something's fishy" is true. No, I can't insist that the probability to see another head is still $\frac{1}{2}$

I'll leave it to you to apply Bayesian approach and get to a similar conclusion. You'll start with prior probability of heads $p=\frac{1}{2}$, then update it with observation of 10 heads in a row, and you'll see how posterior probability of heads $\pi>\frac{1}{2}$

UPDATE @oerkelens example can be interpreted in two ways.

• your friend bet on THHTTHTTHT, then tossed a coin 10 times and got: THHTTHTTHT. In this case you'll be as surprised as with 10 heads in a row, and start doubting the fairness of a coin. You're not sure what to think about the probability of tail in the next toss, because your friend seems to be able to get exactly what he wants, this is not random.
• you threw a coin 10 times, and observed some combination which happened to be THHTTHTTHT, you'll notice there were 6 tails and 4 heads, which is $p=\frac{10!}{6!4!2^{10}}\sim 0.2$, which is unremarkable. Hence, the probability of a tail in the next toss is probably $\frac{1}{2}$, since there's no reason to doubt its fairness.

Also, one could argue that although 0.001 is a small probability, if you toss 10 coins 100,000 times, you're bound to see a few 10-head combinations. True, but in this case you have 1 million coin tosses in total, and you're looking for at least one 10-head combination in the sequence. The frequentist probability of observing at least one 10-head combination is computed as follows: $$1-\left(\frac{1}{2^{10}}\right)^{100,000}\approx 1$$ So, the frequentist will conclude after long months of tossing a coin 1 million times and observing a 10-head combination, that it's no big deal, things happen. He will not be making any adjustments to his expectations about the probability of the next head, and leave it at 0.5

FOR COMPUTER PEOPLE If your friends are computer programmers then I found that the easiest way to appeal to their intuition is through programming. Ask them to program the coin toss experiment. They'll think a little bit then come up with something like this:

for i=1:11
   if rand()>0.5 
       c='H';
   else
       c='T';
   end
   fprintf('%s',c)
end
disp '.'

THTHTHTHHHT.

You'll ask them

where's your code for handling 10 heads in a row here? It appears that in your code regardless of what happened in first 10 loops, the 11th toss has 0.5 probability of heads.

However, this case appeals to the fair coin toss. The code is designed with a fair coin toss. In case of 10 heads though, it's highly unlikely that the coin is fair.

Answer 10

Under ideal circumstances the answer is no. Each throw is independent of what came before. So if this is a truly fair coin then it does not matter. But if you unsure about whether the coin is faulty or not (which could happen in real life), a long sequence of tails may lead one to believe that it is unfair.

Answer 11

This answer will work for all questions of this sort, including the Monty Hall problem. Simply ask them what they think the odds are of getting a tail after ten heads. Offer to play them for slightly better (to them) but still under 50-50 odds. With any luck they will agree to let a computer do the flipping in which case you will quickly have a sum of money in your pocket. Otherwise it will take longer but the result is (inevitably) the same.

Answer 12

How would you convince them? One way is to show the distribution of outcomes from the exact problem described.

#1,000,000 observations
numObservations <- 1e+6
#11 coin tosses per sample
numCoinTosses <- 11

sampledCoinTosses <- matrix(sample(c(-1,1),numObservations*numCoinTosses,replace=TRUE),
                        nrow = numObservations, ncol = numCoinTosses)
sampledCoinTosses <- cbind(sampledCoinTosses,apply(sampledCoinTosses[,1:numCoinTosses - 1],1,sum))
#Where the sum of the first ten observations is 10, this corresponds to 10 heads.
tenHeadsObservations <- sampledCoinTosses[which(sampledCoinTosses[,numCoinTosses + 1] == 10),]
#By looking at the summary of the 11th coin toss we can see how close the average value is to 0
summary(tenHeadsObservations[,numCoinTosses])

Answer 13

Try like this: Assume that we already have $10$ heads tosses -- a very very rare event with probability of "being there" of $0.5^{10}$. Now we prepare for one more toss, and think ahead what might happen next:

• if tails, we still end up with recording an extremely rare series of events with probability of $0.5^{10}$;
• if heads, the probability of whole series is somewhat smaller, but not That much smaller, $0.5^{11}$;

And the difference between the two is just one fair coin toss.