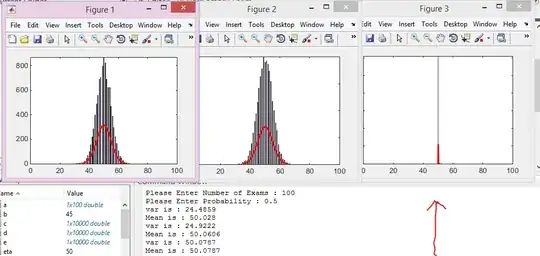
i using bionrnd() function to generate a random vector and Laplace approximation formula to approximate the binomial distribution. but Laplace histogram dose not like the binomial distribution histogram.
where is my mistake in coding?
help me please and here is my code :
clear
clc
close all
n = input ('Please Enter Number of Exams : ');
p = input ('Please Enter Probability : ');
eta=n*p;
sigma=sqrt(n*p*(1-p));
for x=1:n*100;
a=rand(1,n);
b=0;
for i=1:n
if(a(i)>=1-p)
b=b+1;
end
end
c(x)=b;
d(x)=binornd(n , p);
e(x)=(1./(sqrt(2*pi*x*p*(1-p)))).* exp(-(((x+1)*p-(x*p)).^2)./(2*x*p*(1-p)));
end
E=sigma*e+eta;
histfit(c);
axis([0 n 0 inf])
M = mean(c);
varc=var(c);
disp(['var is : ', num2str(varc)]);
disp(['Mean is : ', num2str(M)]);
figure
histfit(d);
axis([0 n 0 inf])
M2 = mean(d);
varc2=var(d);
disp(['var is : ', num2str(varc2)]);
disp(['Mean is : ', num2str(M2)]);
figure
histfit(e,100);
axis([0 n 0 inf])
M3 = mean(e);
varc3=var(e);
disp(['var is : ', num2str(M3)]);
disp(['Mean is : ', num2str(M3)]);
the e(x) is formula of Laplace approximation in this link : De Moivre Laplace theorem formula
output is :