1

Basic question: In a two independent sample test of differences in means, is it possible to have a one sided hypothesis?

Typically, when you have 2 groups the two sample test only tests whether the means are the different. But I would like to test whether 1 group is larger than the other.

user13441344
  • 125
  • 1
  • 7
  • That is exactly the case in which you use a one-sided [Mann–Whitney U test](https://en.wikipedia.org/wiki/Mann%E2%80%93Whitney_U_test), for example. – Avraham Jan 29 '15 at 03:16

1 Answers1

3

Yes, certainly you can have a one-sided hypothesis test for equality of two means.

Most commonly people use a two-sample t-test for the equality of two means (with or without the Welch adjustment to d.f. for different variances), but there are alternatives, including a permutation test.

A one-sided two sample test works analogously to the one-sample case.

Here's an example, done in R on Fisher's sleep data:

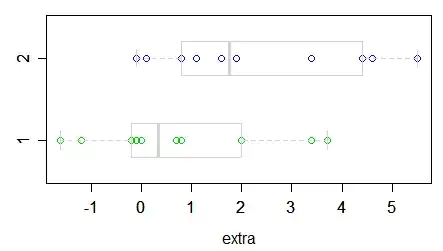
enter image description here

> t.test(extra~group, data=sleep, alternative="less")

        Welch Two Sample t-test

data:  extra by group
t = -1.8608, df = 17.776, p-value = 0.0397
alternative hypothesis: true difference in means is less than 0
95 percent confidence interval:
       -Inf -0.1066185
sample estimates:
mean in group 1 mean in group 2 
           0.75            2.33

The equal-variance version gives almost the same p-value (0.0396)

If you want to test whether the values tend to be larger in one population than another, in the sense that your alternative is of the form $P(X>Y)>\frac12$ then you could use a Wilcoxon-Mann-Whitney for that.

Glen_b
  • 257,508
  • 32
  • 553
  • 939