3

I'm fitting a multiple linear regression model. I've read that the residuals of my regression need to be normally distributed in order for the p and t values to be accurate. Now my residuals (see below) have very high Kurtosis (8.02). What kind of adjustments do I have to make to still be able to use my data?

enter image description here

enter image description here

Simontheguest
  • 41
  • 1
  • 1
  • 3
  • 2
    Short answer is that we can't reliably say from this information. But from the hints here measured skewness and kurtosis may reflect, most of all, one or more outliers for which predicted > observed. – Nick Cox Jan 26 '15 at 16:44
  • 1
    From the QQ plot, the single outlier (large negative residual) seems to be the main cause of the kurtosis. So I'd ignore the kurtosis and think about that instead. Aside from that point, the rest look reasonable -- but you can't properly judge this issue (is it really a problem? how much?) if there's problems in some of the other diagnostics. In particular, this will be an influential point as well (though I can't judge the extent) and the impression might be impacted by possible lack of fit or the potential presence of heteroskedasticity, which should be assessed first. – Glen_b Jan 26 '15 at 22:25
  • hey glen, thank you for the feedback. I had issues with heteroskedasticity, which is why applied the natural logarithm (+constant as I had negative value) to the dependent variable. I was researching a lot on what to do with heteroscedastic patterns in my residuals and applying the natural log was often mentioned and seemed like a good method to me in order to keep adjustments to a minimum. I don't want to exclude the outliers in the dependent variable, because I'm looking at extreme first day returns of IPOs, so looking at extreme value is part of my research. – Simontheguest Jan 27 '15 at 15:45
  • Regarding outliers in the independent variables I'm not sure how to identify them. would the outlier labeling rule by Hoaglin be appropriate? – Simontheguest Jan 27 '15 at 15:47

1 Answers1

5

I agree with @Nick Cox. Here are a couple of thoughts to help you move forward:

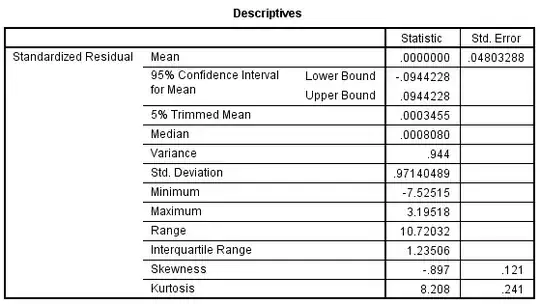
  1. It's better to assess the standardized residuals for normality rather than the unstandardized residuals, as you do here. (You might also benefit from reading my answer here: Interpreting plot.lm().)
  2. It is somewhat problematic to interpret kurtosis in the presence of skewness. (There is good information on skewness and kurtosis here.) Although the skewness of your sample may see only 'moderate' by conventional schemes (i.e., between -.5 and -1), the standard error of the skewness is .121, so your sample is 7.4 SEs from 0. Note that your minimum value (-4) is much further from your mean than your maximum value (1.7), and the mean (0) is below your trimmed mean (0.0002), which is below your median (0.0004).

Some suggestions:

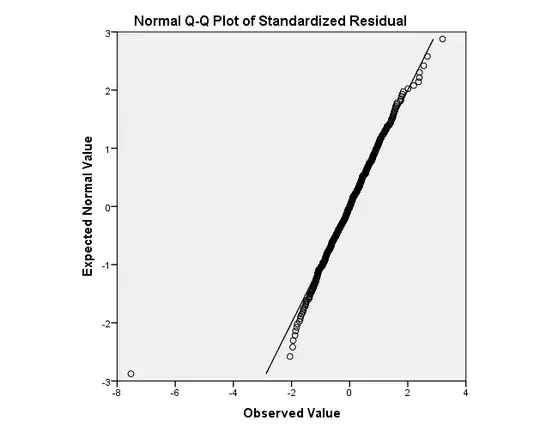
  1. Try assessing the standardized residuals, and also look at a qq-plot. (@Glen_b has a nice display of various possibilities for qq-plots here: How to interpret a QQ plot. I have also provided some information on the construction and interpretation of qq-plots here: QQ plot does not match histogram, and here: PP-plots vs. QQ-plots. Note that these three answers assume the theoretical distribution is on the x-axis and your data are on the y-axis, which is flipped relative to your plot.)

    a. If you seem to have a couple outliers, but the rest of the distribution seems fine, try using robust regression. (You may want to search / read through some of the threads already on CV categorized under the tag.)

    b. If the whole distribution is skewed in a smooth and continuous way, you might try a transformation, such as from the Box-Cox family of transformations, and use standard regression methods with the transformed data.

Update 1: Because the 5% trimmed mean is closer to the untrimmed mean than the median even with the standardized residuals, I suspect b will be the more appropriate option. The qq-plot will give us more information, though.

Update 2: Your biggest issue is a single outlier. You could use robust regression, but you may still have a problem with skewness nonetheless. Try a qq-plot and descriptives for your standardized residuals without that point.

Community
  • 1
gung - Reinstate Monica
  • 132,789
  • 81
  • 357
  • 650
  • Thank you so much for your feedback! I have now posted the standardized residuals instead of the unstandardized ones. Should I generate the QQ plot for the standardized residuals or for the variables of the regression? – Simontheguest Jan 26 '15 at 18:30
  • @Simontheguest, you should generate a qq-plot for the standardized residuals. – gung - Reinstate Monica Jan 26 '15 at 18:33
  • 1
    I would warn Simon that my QQ plots are flipped around from the one he shows. That is, I always put the expected (which are fixed, given n) on the x-axis and the actual (the random variable) on the y -- so all those must be transposed when interpreting the QQ plot here. – Glen_b Jan 26 '15 at 22:29