Does skewness predicts variance?

Question

(with apologizes to this question).

Consider two distributions $G$, $F$ both uni-modal and absolutely continuous, square integrable and satisfying:

$$F<_c G$$

this means that the standardized distributions $F(x\sigma_F+\mu_F)$ and $G(x\sigma_G+\mu_G)$ cross each other exactly twice and that in the middle section we have that $G(x\sigma_G+\mu_G)>F(x\sigma_F+\mu_F)$, as in the example below (from [0]):

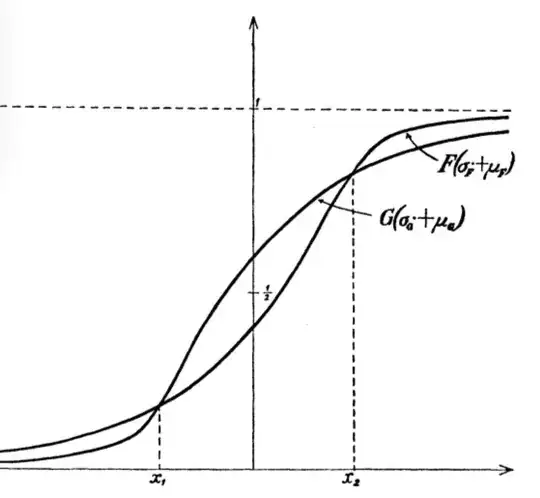
In practice, $F<_c G$ is a convenient way to say that $G$ is more right skewed than $F$.

Now, can we say that:

$$F<_c G\implies \sigma_G^2\geq \sigma_F^2$$

? I couldn't find a proof of this,

---

From wiki:

If the random variable $X$ is continuous with probability density function $f(x)$, then the variance is given by

$$\sigma^2_F =\int (x-\mu)^2 \, f(x) \, dx\, =\int x^2 \, f(x) \, > dx\, - \mu^2$$

where $\mu_F$ is the expected value, $$\mu_F = \int x \, f(x) \, dx\, $$

• [0]Hannu Oja (1981). On Location, Scale, Skewness and Kurtosis of Univariate Distributions. Scandinavian Journal of Statistics, Vol. 8, No. 3 (1981), pp. 154-168

Answer 1

It may depend on how one measures skewness, but if we adopt the usual standardized third moment as a measure of skewness, then the answer is "No", at least not in general: higher skewness may imply lower variance.

Consider the case of chi-squared distributions. A chi-square has variance $\sigma^2=2k$ and skewness coefficient $\gamma_1=\sqrt {8/k}$, where $k$ is the number of degrees of freedom.

Then if we have two chi-squares and it holds that

$$\gamma_{1(X)} = \sqrt {8/k_X} > \sqrt {8/k_Y}=\gamma_{1(Y)}$$

we are led to

$$\sqrt {8/k_X} > \sqrt {8/k_Y} \Rightarrow 2k_Y = \sigma^2_Y > \sigma^2_X = 2k_X $$

This may appear counter-intuitive at first: after all as variance increases the right tail spreads more to the right, becomes fatter, so shouldn't also skewness increase?

I would say no, because the purpose here is not to have two different measures for the same thing, and this is I think why we use a skewness measure that it is, exactly, standardized with respect to the variance: to my understanding, skewness attempts to measure the relative degree of the fatness of a tail compared to the "tightness" of the remaining part of the distribution.

In the chi-square example, the third central moment unstandardized is a linear function of the variance -the higher the variance, the higher it will also be. But do we obtain any additional useful information this way? I wouldn't say so. But standardized it reveals that the opposite relation holds (higher variance implies lower skewness), and if one looks at the plots of chi-square densities as the degrees of freedom (and hence the variance) increase, I believe he may get the visual intuition as to why this is not so counter-intuitive after all: as the right tail gets thicker and spread out more to the right, the remaining part of the distribution gets less and less "uptight" (and at a "faster rate" as the skewness coefficient reveals).