Criteria for signal registration

Question

I want to find statistical criteria for signal registration (see pict). When I don't have a signal I registrate a simple gaussian two-dimenshial distribution. When I have a signal I have gaussian plus some "tail" (horizontal on the picture). Direction of a "tail" may differs, but I have some minimum length of a tail for a proper signal.

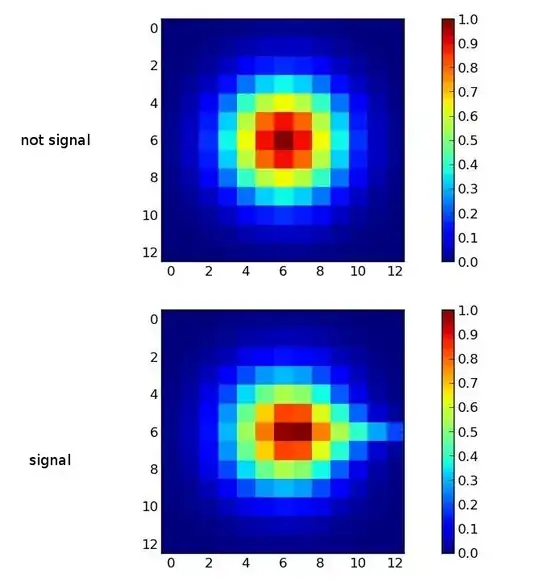
I tried to use chi square criteria but faild. p-value for my signal was 1.0. What kind of a criteria can I use in this case?

There is a sample data:

A signal:

[[ 0.    0.    0.    0.01  0.01  0.01  0.02  0.01  0.01  0.01  0.    0.    0.  ]
 [ 0.    0.    0.01  0.02  0.03  0.05  0.05  0.05  0.03  0.02  0.01  0.    0.  ]
 [ 0.    0.01  0.02  0.05  0.09  0.13  0.14  0.13  0.09  0.05  0.02  0.01  0.  ]
 [ 0.01  0.02  0.05  0.11  0.2   0.27  0.31  0.28  0.2   0.11  0.05  0.02  0.01]
 [ 0.01  0.03  0.09  0.2   0.34  0.48  0.56  0.52  0.37  0.21  0.1   0.03  0.01]
 [ 0.01  0.05  0.13  0.27  0.48  0.69  0.84  0.83  0.62  0.4   0.22  0.08  0.03]
 [ 0.02  0.05  0.14  0.31  0.54  0.78  0.99  1.    0.77  0.56  0.4   0.29  0.19]
 [ 0.01  0.05  0.13  0.27  0.48  0.69  0.84  0.83  0.62  0.4   0.22  0.08  0.03]
 [ 0.01  0.03  0.09  0.2   0.34  0.48  0.56  0.52  0.37  0.21  0.1   0.03  0.01]
 [ 0.01  0.02  0.05  0.11  0.2   0.27  0.31  0.28  0.2   0.11  0.05  0.02  0.01]
 [ 0.    0.01  0.02  0.05  0.09  0.13  0.14  0.13  0.09  0.05  0.02  0.01  0.  ]
 [ 0.    0.    0.01  0.02  0.03  0.05  0.05  0.05  0.03  0.02  0.01  0.    0.  ]
 [ 0.    0.    0.    0.01  0.01  0.01  0.02  0.01  0.01  0.01  0.    0.    0.  ]]

Not a signal:

[[ 0.    0.    0.    0.01  0.01  0.02  0.02  0.02  0.01  0.01  0.    0.    0.  ]
 [ 0.    0.    0.01  0.02  0.04  0.06  0.06  0.06  0.04  0.02  0.01  0.    0.  ]
 [ 0.    0.01  0.03  0.06  0.11  0.15  0.17  0.15  0.11  0.06  0.03  0.01  0.  ]
 [ 0.01  0.02  0.06  0.14  0.24  0.33  0.37  0.33  0.24  0.14  0.06  0.02  0.01]
 [ 0.01  0.04  0.11  0.24  0.41  0.57  0.64  0.57  0.41  0.24  0.11  0.04  0.01]
 [ 0.02  0.06  0.15  0.33  0.57  0.8   0.9   0.8   0.57  0.33  0.15  0.06  0.02]
 [ 0.02  0.06  0.17  0.37  0.64  0.9   1.    0.9   0.64  0.37  0.17  0.06  0.02]
 [ 0.02  0.06  0.15  0.33  0.57  0.8   0.9   0.8   0.57  0.33  0.15  0.06  0.02]
 [ 0.01  0.04  0.11  0.24  0.41  0.57  0.64  0.57  0.41  0.24  0.11  0.04  0.01]
 [ 0.01  0.02  0.06  0.14  0.24  0.33  0.37  0.33  0.24  0.14  0.06  0.02  0.01]
 [ 0.    0.01  0.03  0.06  0.11  0.15  0.17  0.15  0.11  0.06  0.03  0.01  0.  ]
 [ 0.    0.    0.01  0.02  0.04  0.06  0.06  0.06  0.04  0.02  0.01  0.    0.  ]
 [ 0.    0.    0.    0.01  0.01  0.02  0.02  0.02  0.01  0.01  0.    0.    0.  ]]

Answer 1

There is a problem with your sampling method. Your noise floor is too high or your signal is to weak. If you have the option, recalibrate your instruments/simulation and improve the signal to noise ratio (If you are using some kind of amplifier, turn down the gain.). The only statistical criterion that is able to distinguish the two images, as you hinted at yourself, is a measure of skewness (two for two tails). However, if you have constant predictable noise you could simply subtract the noise from the signal+noise to extract the signal, but this requires that the noise sample you subtract is representative of noise over time and is not fluctuating too much. Something similar could be achieved with an (online) filter. Your error term is much larger than your factor term, so it is like searching for a needle in a hay stack. I think even pattern analysis would be difficult to apply here.

Thanks to @AleksandrBlekh for pointing me to this question.

TLDR: Set up a criterion for skewness and use this as a classifier, unless you can reduce the noise floor during sampling.