I'm analysing data from an experiment in which participants, over a number of trials, were presented with 8 boxes - 7 containing gold coins, and 1 containing a pirate. Their task was to open as many boxes as they liked in each trial, knowing that if they opened too many, they would reveal the pirate, and he would steal back all of the coins. I'm interested in factors which predict risk taking (opening more boxes) in this task.
I planned on fitting a generalized Poisson mixed model, using lme4, with random intercepts and slopes for each participant. However, I may have some issues with the distribution of my data.
Firstly, although the mean is very low (~ 3.5), it's symmetrically distributed, so it's not clear if I need to use a Poisson model at all.
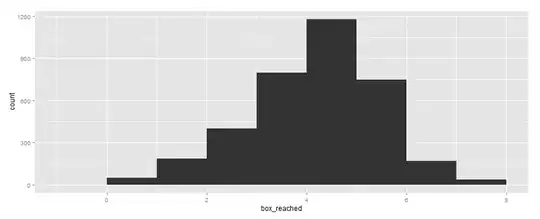
Secondly, it is, by all accounts, hugely underdispersed (unless I'm misunderstanding something).
> mean(data$box_reached)
[1] 3.678992
> var(data$box_reached)
[1] 1.754588
# Alternative test of dispersion
# > 1 indicates overdispersion
# (I assume < 1 indicates underdispersion)
# https://stat.ethz.ch/pipermail/r-sig-mixed-models/2011q1/012632.html
> rdev = sum(residuals(glm.2)^2)
> mdf = length(fixef(glm.2))
> rdf = nrow(keep_keep) - mdf
> rdev/rdf
[1] 0.3799419
Searching around, I've struggled to find an appropriate way of analysing this. I could just use the linear model (which yields marginally lower p values), I could run the Poisson regression as-is, or I could look further into beta regression, or survival analyses, or ordinal regression?
(This question suggests a zero-inflated model, but that's clearly not appropriate for my model, where 0s are the consequence of mistakes by participants.)