Many statistics textbooks state that adding more terms into a linear model always reduces the sum of squares and in turn increases the r-squared value. This has led to the use of the adjusted r-squared. But is it possible that adding a term into a linear model reduces the sum of squares by zero and in turns keep the r squared value exactly the same?
-
2The correct statement about $R^2$ is that adding new parameters does not reduce it. It doesn't have to be a strict increase. – Aksakal Jan 12 '15 at 14:03
-
@Aksakal have you worded that correctly? – luciano Jan 12 '15 at 14:05
-
See the explanation [here](http://en.wikipedia.org/wiki/Coefficient_of_determination#Inflation_of_R2). They call it *nondecreasing* property – Aksakal Jan 12 '15 at 14:08
2 Answers
Certainly this can happen: if the new predictor is contained in the linear span of the predictors already in the model.
Think about it geometrically: your new "fitting subspace" (the possible linear combinations of your predictors) is exactly the same as the old one, so the optimal fit and the sum of squares is unchanged.
However, this is only a sufficient condition for $R^2$ to be unchanged, not a necessary one. Consider three points like this:
xx <- c(-1,0,1)
yy <- c(1,-2,1)
plot(xx,yy,pch=19)
abline(h=0)
abline(v=0)
model.1 <- lm(yy~1)
abline(model.1,col="red",lty=2)
summary(model.1)
model.2 <- lm(yy~xx)
abline(model.2,col="green",lty=3)
summary(model.2)
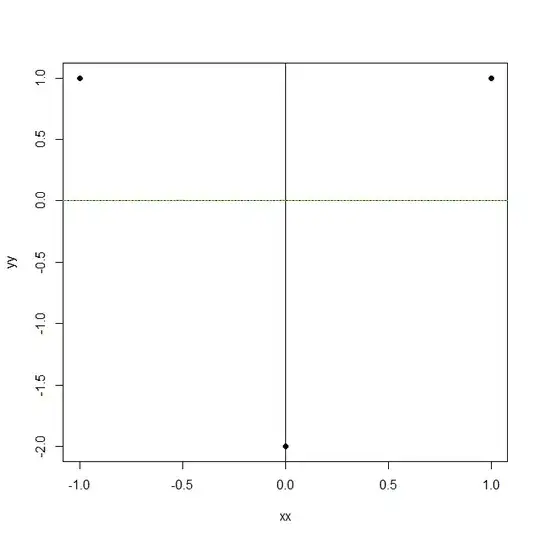
If we add xx as a predictor to the simple mean model, we get the same fit and the same $R^2$. Such a construction should be possible with larger models, as well.
- 95,027
- 13
- 197
- 357
-
1But if the predictor has different values to predictors already in the model but absolutely no relationship with the response variable, will the r-squared stay the same? – luciano Jan 12 '15 at 11:42
-
-
-
I changed my answer, I was wrong about the "necessary" part. I'd assume that there is some geometric interpretation of updating OLS with a new predictor (scalar products between the new predictor and residuals of the smaller model?) that quantifies your "no" in a way that $R^2$ would be unchanged when adding a predictor. – Stephan Kolassa Jan 12 '15 at 12:10
-
If the new predictor is a linear combination of the previous ones, then isn't your least squares solution no longer unique since $X$ is no longer full rank and thus $(X^TX)^{-1}$ is singular? – 24n8 Aug 17 '20 at 17:19
-
@Iamanon: yes, the solution is no longer unique. But the *fit* won't change, and that is what $R^2$ is calculated from. – Stephan Kolassa Aug 17 '20 at 18:22
-
@StephanKolassa Right, but I'm kind of confused about this case. $R^2$ depends on the sum of residuals, which depends on $\hat{y}_i$, which depends on $\hat{\beta}$. If $\hat{\beta}$ isn't unique, how is $R^2$ computed? In this case, is it that $R^2$ is the same for any set of $\hat{\beta}$ in the non-unique set? – 24n8 Aug 17 '20 at 18:26
-
1The point is that even in an undetermined system, the betas may be different, but the fits $\hat{y}_i$ will be the same, and therefore also the $R^2$. – Stephan Kolassa Aug 17 '20 at 18:41
Adding more terms into a linear model may keep the r squared value exactly the same or increase the r squared value. It is called non-decreasing property of R square.
To demonstrate this property, first recall that the objective of least squares linear regression is $$ min{SSE}=min\displaystyle\sum\limits_{i=1}^n \left(e_i \right)^2= min_{\beta}\sum_{i=1}^n\left(y_i -\beta_0 - \beta_1x_{i,1} - \beta_2x_{i,2} -…- \beta_px_{i,p}\right)^2 $$ R square is $$ R^2=1-\frac{SSE}{SST} $$ When the extra variable is included, the objective of least squares linear regression becomes $$ min{SSE}=min_{\beta}\sum_{i=1}^n\left(y_i -\beta_0 - \beta_1x_{i,1} - \beta_2x_{i,2} -…- \beta_px_{i,p}-\beta_{p+1}x_{i,p+1}\right)^2 $$ If extra estimated coefficient($\beta_{p+1}$) is zero, the SSE and the R square will stay unchanged. Or if extra estimated coefficient($\beta_{p+1}$) takes a nonzero value , the SSE will reduce. In this case, the R square will increase, because it improves the quality of the fit.
- 111
- 1
- 7
-
I think your conclusion is not quite right, because it makes a critical unstated assumption: if the extra estimated coefficient is zero *and if the estimates of the other coefficients do not change,* then $R^2$ will remain the same. Also, it is possible for the extra estimated coefficient to be nonzero, yet the $R^2$ will not change. (This happens when the new variable lies within the span of the previous variables.) The logic of the demonstration is simpler than this: by *setting* $\hat\beta_{p+1}=0$ you will obtain the same solution as before, whence it is impossible to do any worse. – whuber Apr 09 '19 at 21:24
-
@whuber When extra estimated coefficient is nonzero, the estimates of the other coefficients have to change to minimize the cost function. Cost function in linear regression is a convex function, so once parameters change, the cost function can not stay unchanged. If cost function change, it can only reduce. – DavidCruise Apr 09 '19 at 21:57
-
1I'm afraid that's not always the case. You implicitly assume the new variable does not lie in the span of the existing ones. When it does, the cost function is not strictly convex and adding the variable accomplishes nothing. – whuber Apr 09 '19 at 21:59
-
@whuber When $\beta_{p+1}=\hat\beta_{p+1}\ne0$ is the solution for minJ(X), $\beta_{p+1}=0$ is not the solution for minJ(X). $\Rightarrow\frac{\partial{J(X)}}{\partial{\beta_{p+1}}}|_{\beta_{p+1}=0}\ne0\Rightarrow$ There must exist point around 0 which is less than $minJ(X)|_{\beta_{p+1}=0}$. $\Rightarrow J(X)|_{\beta_{p+1}=\hat\beta_{p+1}}
– DavidCruise Apr 10 '19 at 00:07 -
@whuber If the new variable lies in the span of the existing ones, then I don't think you can say anything about $R^2$ in this case. In DavidCruise's answer above, he said that $R^2$ would remain the same if the new variable is a linear combination of the previous ones. But the problem is now ill-posed / singular, so you could have an infinite number of solution sets for the $\hat{\beta}$'s. There's no guarantee that $R^2$ would be the same for all of these solution sets, and for the solution without the newly added dependent variable, right? – 24n8 Aug 17 '20 at 18:04
-
@Iamanon I think you ignore the fact that $R^2$ doesn't care about the coefficients: it is a function of the distance from the response vector to the space spanned by the columns of the model matrix. From this perspective the situation is perfectly well posed, even if there might be multiple ways to estimate the coefficients -- and it should now be obvoius that $R^2$ will be the same. – whuber Aug 17 '20 at 18:09
-
@whuber Doesn't it implicitly care about the coefficients? Since $$ R^2 = 1 - \frac{SS_{res}}{SS_{tot}} $$ Here, $SS_{res} = \sum_i (\hat{y}_i - y_i)$, but $\hat{y}_i$ is a function of $\hat{\beta}$? – 24n8 Aug 17 '20 at 18:11
-
1@Iamanon Notice the numerator depends only on the *residuals.* That sum of squares of residuals is the squared distance from the response to the column space. This description makes it obvious that $SS_\text{res}$ does not depend on the actual values of the coefficients. – whuber Aug 17 '20 at 19:25
-