Non-transitivity of correlation: correlations between gender and brain size and between brain size and IQ, but no correlation between gender and IQ

Question

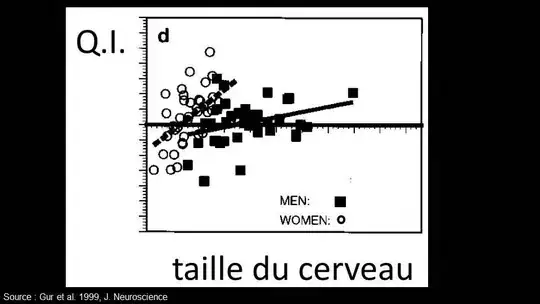
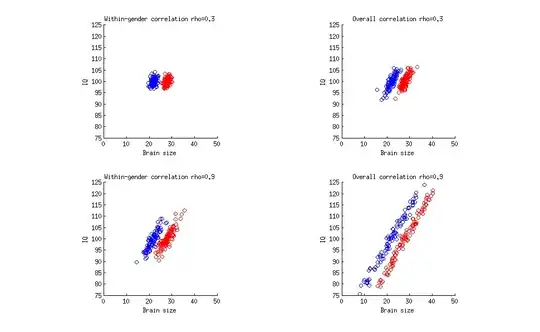
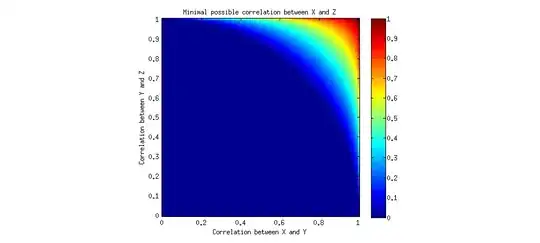
I found a following explanation on a blog and I would like to get more information about the non-transitivity of correlation:

We have the following indisputable facts:

• On average, there is a difference in brain volume between men and women
• There is a correlation between IQ and brain size; the correlation is 0.33 and thus corresponds to 10% of the variability of IQ

From these premises 1 and 2, it seems to follow logically from that: women on average have a lower IQ than men. But it is a fallacy! In statistics, correlations are not transitive. The proof is that you just need to look at the results of IQ tests, and they show that the IQ of men and women do not differ on average.

I would like to understand this non-transitivity of correlation a bit deeper.

If the correlation between IQ and brain size was 0.9 (which I know it isn't (1)), would deducing that women on average have a lower IQ than men would still be a fallacy?

Please, I am not here to talk about IQ (and the limits of the test), sexism, woman stereotype, arrogance and so on (2). I just want to understand the logical reasoning behind the fallacy.

---

(1) which I know it isn't: Neanderthals had bigger brains than homo sapiens, but were not smarter;

(2) I am a woman and overall, I don't consider myself, or the other women less smart than men, I don't care about IQ test, because what count is the value of people, and it's not based on the intellectual abilities.

---

The original source in French:

On a les faits indiscutables suivants:

• il y a une différence de volume cérébral en moyenne entre hommes et femmes
• il y a une corrélation entre QI et volume cérébral; la corrélation est 0.33 et correspond donc à 10% de la variabilité

De ces prémisses 1 et 2, il semble découler logiquement que: les femmes ont en moyenne un QI inférieur aux hommes.

Mais c'est une erreur de raisonnement! En statistique, les corrélations ne sont pas transitives. La preuve, c'est que pour en avoir le cœur net, il suffit de regarder les résultats des tests de QI, et ceux-ci montrent que les QI des hommes et des femmes ne diffèrent pas en moyenne.

Answer 1

Yes, it would still be a fallacy.

Here is a very simple figure showing four different situations. In each case red dots represent women, blue dot represent men, horizontal axis represents brain size and vertical axis represents IQ. I generated all four datasets such that:

• there is always the same difference in mean brain size between men ($22$) and women ($28$ - units are arbitrary). These are population means, but this difference is big enough to be statistically significant with any reasonable sample size;

• there is always zero difference in mean IQ between men and women (both $100$), and also zero correlation between gender and IQ;

• the strength of correlation between brain size and IQ varies as shown on the figure.

In the upper-left subplot within-gender correlation (computed separately over men and separately over women, then averaged) is $0.3$, like in your quote. In the upper-right subplot overall correlation (over men and women together) is $0.3$. Note that your quote does not specify what the number of $0.33$ refers to. In the lower-left subplot within-gender correlation is $0.9$, like in your hypothetical example; in the lower-right subplot overall correlation is $0.9$.

So you can have any value of correlation, and it does not matter if it's computed overall or within-group. Whatever the correlation coefficient, it is very well possible that there is zero correlation between gender and IQ and zero gender difference in mean IQ.

---

Exploring the non-transitivity

Let us explore the full space of possibilities, following the approach suggested by @kjetil. Suppose you have three variables $x_1, x_2, x_3$ and (without loss of generality) suppose that correlation between $x_1$ and $x_2$ is $a>0$ and correlation between $x_2$ and $x_3$ is $b>0$. The question is: what is the minimal possible positive value of the correlation $\lambda$ between $x_1$ and $x_3$? Does it sometimes have to be positive, or can it always be zero?

The correlation matrix is $$\mathbf R = \left( \begin{array}{} 1&a&\lambda \\ a&1&b \\ \lambda &b&1 \end{array}\right)$$ and it has to have a non-negative determinant, i.e. $$\mathrm{det} \mathbf R = -\lambda^2 + 2ab\lambda - ( a^2+b^2-1) \ge 0,$$ meaning that $\lambda$ has to lie between $$ab \pm \sqrt{(1-a^2)(1-b^2)}.$$ If both roots are positive, then the minimal possible value of $\lambda$ is equal to the smaller root (and $\lambda$ has to be positive!). If zero is between these two roots, then $\lambda$ can be zero.

We can solve this numerically and plot the minimal possible positive value of $\lambda$ for different $a$ and $b$:

Informally, we could say that correlations would be transitive if given that $a>0$ and $b>0$, one could conclude that $\lambda>0$. We see that for most of values $a$ and $b$, $\lambda$ can be zero, meaning that correlations are non-transitive. However, for some sufficiently high values of $a$ and $b$, correlation $\lambda$ has to be positive, meaning that there is "some degree of transitivity" after all, but restricted to very high correlations only. Note that both correlations $a$ and $b$ have to be high.

We can work out a precise condition for this "transitivity": as mentioned above, the smaller root should be positive, i.e. $ab - \sqrt{(1-a^2)(1-b^2)}>0$, which is equivalent to $a^2+b^2>1$. This is an equation of a circle! And indeed, if you look at the figure above, you will notice that the blue region forms a quarter of a circle.

In your specific example, correlation between gender and brain size is quite moderate (perhaps $a=0.5$) and correlation between brain size and IQ is $b=0.33$, which is firmly within the blue region ($a^2+b^2<1$)meaning that $\lambda$ can be positive, negative, or zero.

---

Relevant figure from the original study

You wanted to avoid discussing gender and brains, but I cannot help pointing out that looking at the full figure from the original article (Gur et al. 1999), one can see that whereas there is no gender difference in verbal IQ score, there is an obvious and significant difference in spatial IQ score! Compare subplots D and F.

Answer 2

Let us define $x_1=\text{IQ}, x_2=\text{gender}$ and $x_3$ be some other variable (like brain volume) correlated to both. Let us assume that $$ \text{cor}(x_1, x_2)=\lambda, \\ \text{cor}(x_1,x_3)=\text{cor}(x_2, x_3)=\rho=0.9 $$ What is the smallest possible value for $\lambda$? A correlation matrix must be positive semi-definite, so its determinant must be nonnegative. That can be exploited to give an inequality. Let us try:
The correlation matrix is $$ R=\begin{pmatrix} 1 & \lambda & \rho \\ \lambda & 1 & \rho \\ \rho & \rho & 1 \end{pmatrix} $$ Then we can calculate the determinant of $\rho$ by expanding along the first row: $$ \det R = 1\cdot (1-\rho^2) - \lambda \cdot (\lambda-\rho^2) + \rho \cdot (\lambda \rho - \rho) \\ = 1-\lambda^2 -2\rho^2 + 2\lambda \rho^2 \ge 0, $$ which leads to the inequality $\rho^2 \le \frac{\lambda+1}{2}$. The value $\rho=0.9$ leads to $ \lambda \ge 0.62$.

Update:

In response to comments I have updated somewhat the answer above. Now, what can we make of this? According to the calculations above, a correlation of 0.9 between IQ and brain volume (much larger than empirical). Then, the correlation between gender and IQ must be at least 0.62. What does that mean? In the comments some say this does not imply anything about mean differences between gender. But that cannot be true! Yes, for normally distributed variables we can assign correlation and means without relations. But gender is a zero-one variable, for such variable there is a relation between correlation and mean differences. Concretely, IQ is (say) normally distributed, while gender is discrete, zero-one. Let us assume its mean $p=0.5$ (realistically). Then a (say) positive correlation means that gender tends to be "higher" (that is, one) if IQ is higher. That cannot happen without there being a mean difference! Let us do the algebra: First, to simplify the algebra, let us center IQ at zero instead of the usual 100. That will not change any correlations or mean differences. Let $\mu_1 = \text{E}(x_1 | x_2=1)$ and $\mu_0 = \text{E}(x_1 | x_2=0)$. With $\mu=\text{E}(x_1)$ this means $\mu=0=\mu_1+\mu_0$ since $\mu_0 = -\mu_1$. We have $x_1 \sim \text{N}(\mu=0, \sigma^2)$ and $x_2$ is Bernoulli with $p=1/2$.
$$ \text{corr}(x_1, x_2) = \frac{\text{E}(x_1-\mu)\text{E}(x_2-p)}{\sigma \cdot \frac12} \\ = \frac{\Delta}{2\sigma} $$ where $\Delta = \mu_1 - \mu_0 = 2\mu_1$. With the usual value (for IQ) $\sigma=10$ this gives that the correlation is equal to $\Delta/20$. So a correlation of 0.62 means an IQ difference of 12.4. So the posters claiming the correlation contain no information about IQ mean difference are wrong! That would be true if gender was a continuous variable, which it obviously not is. Note that this fact is related to the fact that for the binomial distribution, variance is a function of the mean (as it must be, since there is only one free parameter to vary). What we have done above is really extending this to covariance/correlation.

But, according to the OP, the true value of $\rho=0.33$. Then the inequality becomes that $\lambda \ge -0.7822$, so $\lambda=0$ is a possible value. So in the true case, no conclusions about mean differences in IQ can be drawn from the correlation between IQ and brain volume.

Answer 3

This is a situation in which I like using path diagrams to illustrate direct effects and indirect effects, and how those two impact the overall correlations.

Per the original description we have a correlation matrix below. Brain size has around a 0.3 correlation with IQ, female and IQ have a 0 correlation with each other. I fill in the negative correlation between female and brain size to be -0.3 (if I had to guess it is much smaller than that, but this will serve for illustration purposes).

       Brain  Female  IQ
 Brain   1
Female  -0.3    1
    IQ   0.3    0      1

If we fit a regression model where IQ is a function of brain size and being female we can illustrate this in terms of a path diagram. I have filled in the partial regression coefficients on the arrows, and the B node stands for brain size and the F node stands for female.

Now how crazy is that -- when controlling for brain size, given these correlations, female's have a positive relationship with IQ. Why is this, when the marginal correlation is zero? Per rules with linear path diagrams (Wright, 1934), we can decompose the marginal correlation as a function of the direct effect when controlling for brain size and the indirect effect:

$$\text{Total}_{\text{F},\text{IQ}} = \text{Direct}_{\text{F},\text{IQ}} + \text{Indirect}_{\text{F},\text{B},\text{IQ}}$$

In this notation $\text{Total}_{\text{F},\text{IQ}} = \text{Cor}(\text{F},\text{IQ})$. So per the original definition we know this total effect to be zero. So now we just need to figure out the direct effect and the indirect effect. The indirect effect in this diagram is simply following the other arrow from females to IQ through brain size, which is the correlation of females and brain size multiplied by the partial correlation of brain size and IQ.

\begin{align} \text{Indirect}_{\text{F},\text{B},\text{IQ}} &= \text{Cor}(\text{F},\text{B}) \cdot \text{Cor}(\text{B},\text{IQ}|\text{F}) \\ -0.099 &= -0.3 \cdot 0.33 \end{align}

Because the total effect is zero, we know that the direct effect must simply be the exact opposite sign and size of the indirect effect, hence the direct effect equals 0.099 in this example. Now, here we have a situation when assessing the expected IQ of females we get two different answers, although probably not what you initially expected when specifying the question. When simply assessing the marginal expected IQ of females versus males, the difference is zero as you defined it (by having a zero correlation). When assessing the expected difference conditional on brain size, females have a larger IQ than males.

You can insert into this example either larger correlations between brain size and IQ (or smaller correlations between female and brain size), given the limits kjetil shows in his answer. Increasing the former makes the disparity between the conditional IQ of women and men even greater in favor of women, decreasing the latter makes the differences smaller.

Answer 4

To provide the purely abstract mathematical answer, denote $v$ the brain volume and $q$ the IQ index. Use $1$ to index men and $2$ to index women. Let's assume that the following are facts:

$$E(v_1) > E(v_2) = \beta E(v_1), 0< \beta <1, \;\; \rho(v_1,q_1) >0, \;\; \rho(v_2,q_2)>0 \tag{1}$$

Note that while the quoted text talks about "correlation between brain volume and IQ" in general, the supplied image makes a distinction with the two trend-lines (i.e. it shows the correlation for the two subgroups separately). So we consider them separately (which is the correct way to go).

Then

$$\rho(v_1,q_1) >0 \Rightarrow {\rm Cov}(v_1,q_1)>0 \Rightarrow E(v_1q_1) > E(v_1)E(q_1)$$

$$\Rightarrow \frac {E(v_1q_1)}{E(q_1)} > E(v_1) \tag{2}$$

and

$$\rho(v_2,q_2) >0 \Rightarrow {\rm Cov}(v_2,q_2)>0 \Rightarrow E(v_2q_2) > E(v_2)E(q_2)$$

$$\Rightarrow \frac {E(v_2q_2)}{\beta E(q_2)} > E(v_1) \tag{3}$$

Does the above obtained inequalities necessitate $E(q_1) > E(q_2)$??

To check this assume on the contrary that $E(q_1) = E(q_2) = \bar q \tag {4}$

Then it must be the case that

$$(2),(4) \Rightarrow \frac {E(v_1q_1)}{\bar q} > E(v_1) \tag{5}$$

and that

$$(3),(4) \Rightarrow \frac {E(v_2q_2)}{\beta \bar q} > E(v_1) \tag{6}$$

Well, it certainly can be the case, that inequalities $(5)$ and $(6)$ hold at the same time, and so "equal IQ on average" is perfectly compatible with the initial assumptions that we took as facts.
In fact it could very well happen that we could have a higher average IQ from women than for men, for the same set of facts in $(1)$.

In other words, the correlation assumptions/facts in $(1)$ do not impose any constraint whatsoever about the relation between average IQ's at all. All possible relation between $E(q_1)$ and $E(q_2)$ may hold, and be compatible with the assumptions in $(1)$.