I am trying to fit hierarchical mixture model (using ML and MCMC, but this shouldn't matter) where the linear predictor part contains 17 independent variables. These are habitat variables: for each habitat type I have one variable saying the proportions of the area in 100 m circle which belongs to that particular habitat type.
The thing is that these 17 predictor variables sum up to 1 (i.e. simplex).
Could this be a problem with 1) fitting the model 2) model selection 3) predictions? This is not exactly collinearity (there is no correlation coefficient over 0.4 or under -0.4), but the variables are linearly dependent - the each one could be derived from all the others. If there is too much of a certain habitat, there cannot be a lot of other habitat types.
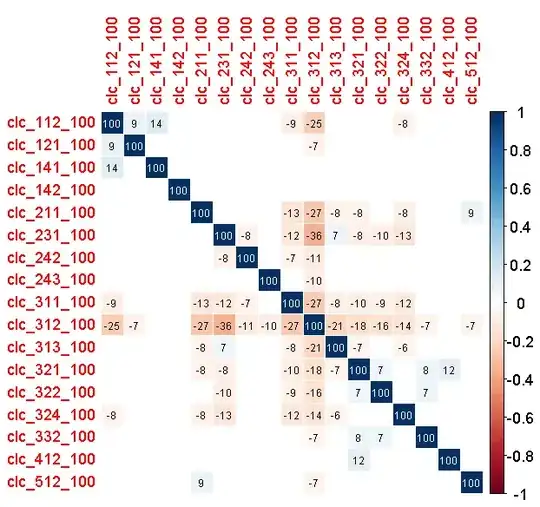
EDIT: The correlogram is here (the number is correlation coefficient multiplied by 100 and rounded. Only significant p < 0.05 coefficients are displayed).
EDIT 2: please do not assume that the variables are correlated. They are slightly in my case, but in general the variables can be linearly dependent but with no correlation! Look at this artificialy generated example:
set.seed(1063)
x <- rmultinom(17, rep(1000, 17), rep(1/17, 17))
envV <- x/1000
(If you have different RNG, please download the generated matrix: http://pastebin.com/sK55w3Y2)
Now the columns of envV are linearly dependent, as they sum up to 1 (see apply(envV, 2, sum)), but they are not correlated. See:
cor.mtest <- function(mat, conf.level = 0.95){
mat <- as.matrix(mat)
n <- ncol(mat)
p.mat <- lowCI.mat <- uppCI.mat <- matrix(NA, n, n)
diag(p.mat) <- 0
diag(lowCI.mat) <- diag(uppCI.mat) <- 1
for(i in 1:(n-1)){
for(j in (i+1):n){
tmp <- cor.test(mat[,i], mat[,j], conf.level = conf.level)
p.mat[i,j] <- p.mat[j,i] <- tmp$p.value
lowCI.mat[i,j] <- lowCI.mat[j,i] <- tmp$conf.int[1]
uppCI.mat[i,j] <- uppCI.mat[j,i] <- tmp$conf.int[2]
}
}
return(list(p.mat, lowCI.mat, uppCI.mat))
}
cor1 <- cor.mtest(envV)
number_of_correlated_variables <- sum(cor1[[1]] < 0.05 & !diag(nrow(cor1[[1]])))
number_of_correlated_variables # reports 0
EDIT 3: It is interesting and strange that the matrix can be actually inverted: if I do solve(t(as.matrix(envV)) %*% as.matrix(envV)) both on my real predictors and the artificial generated ones in EDIT 2, the inverse matrix will get computed with no error or warning (both with solve and ginv()).
Also:
> is.singular.matrix(t(as.matrix(envV)) %*% as.matrix(envV))
[1] FALSE