Let me try to respond your very last question about understanding the Dirichlet distribution, its relation to the Multinomial, and what I suspect is what you really would like to know is how this could be explained in an applied context, such as your genomics problem.
Now I am going to explain all this using my vague recall of haplogroup SNPs, which might be somewhat similar to your data:
- So let's say I have this dataset inspired by this random NIH paper from Homo Sapiens Sapiens and I need to identify all the SNPs associated with this novel sub-sub-subclade of the haplogroup N that I believe exists but I don't know how many of the SNPs (or I guess, another population genetics term would be finding the linkage disequilibrium) there are in each of those 4 sub-sub-clades and what those SNPs are in this Y-DNA sample.
15121 caacagcctt cataggctat gtcctcccgt gaggccaaat atcattctga ggggccacag
15181 taattacaaa cttactatcc gccatcccat acattgggac agacctagtt caatgaatct
15241 gaggaggcta ctcagtagac agtcccaccc tcacacgatt ctttaccttt cacttcatct
15301 tgcccttcat tattgcagcc ctagcagcac tccacctcct attcttgcac gaaacgggat
....etc...etc...`
Given that we do not know the number of SNPs linked together that would fall into this sub-sub-subclade, or the probability of occurence of a SNP in this novel obscure genomic region I'm about to discover, I will treat those unknown parameters as random under the Bayesian paradigm:
I will actually estimate **the number of the linked SNPs ** to be associated with that sub-sub-subclade since I know that if more than 1% of a population does not carry the same nucleotide at a specific position in the DNA sequence, then this variation can be classified as a SNP.
By the "linked SNPs" I mean some unknown number of groups of SNP, such as let's say one possible group we are considering to be associated with this sub-sub-subclade genomic region of haplogroup N would be the group of SNPs for dopaminergic receptors x, y, and z, the other group - for the Serotonin 5-HT2A receptors, which are SNPs rs6311 and rs6313 and so on)
My other parameter will be estimating the expected number of times (denoted by parameter $k$, where $k\ge2$) the outcome SNP $i$ was observed over $N$ sampled nucleotides, where:
$$X_1,\dots,X_k, x_i \in (0,1)$$ a vector of random category counts
$$\sum_{i=1}^N x_i = 1$$,
parametrized by a pseudocount parameter $\boldsymbol{\alpha} = (\alpha_1,\dots,\alpha_k)$
Now, a minute of some math:
- The commonly known probability distributions are related as it is clearly illustrated on the map of the Relationships Among Common Distributions, Adopted from Leemis(1986) from what I call "the Bible of Statistics" every statistician sees vivid dreams about before math stats exams in grad school, a.k.a. the 2nd edition of "Statistical Inference" by G.Casella & R.Berger, 2001. Cengage Learning.. Although even in the extended version of the map from the American Statistician the Dirichlet and Multinomial are not depicted, here is my audacious take on where they would be placed in the classical map #1:
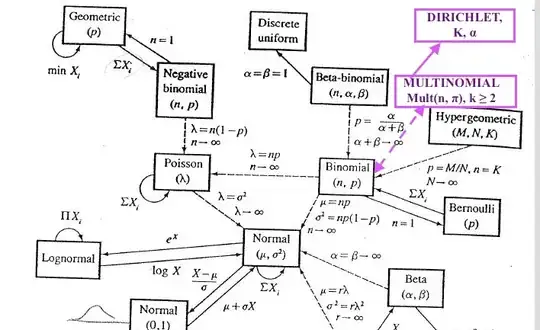
Also, somewhere along those arrows would be another relevant distribution, the Categorical Distribution.
In a nutshell, you can derive or easily transform one of them into the other if they are pretty close on the map and come from the same family of distributions. Some of these are generalizations of other distributions hence, including such as Dirichlet, which is a generalization on the Beta distribution, i.e. Dirichlet generalized the Beta into multiple dimensions.
For this reason and so many others, Dirichlet distribution is the Conjugate Prior for Multinomial Distribution.
Now back to our SNPs problem:
The set up we are going to use for our problem is based on the Pólya urn model where we would sample with replacement $N$ strings of the 4-lettered nucleotide bases that show up in $k$ my-sub-sub-subclade-linked SNPs, where each of SNP of an observed nucleotide bases can be sampled with probabilities $p_1,\dots,p_k$.
Since we don't know how many and which SNPs fall into the the "linked SNPs for this sub-sub-subclade", we would assume those unknown SNPs that may or may not exist for this sub-sub-subclade are represented by a parameter $\alpha$, where he $\alpha_1,\dots,\alpha_k$ and those might actually be the pseudocounts you are referencing. Here is a nice response and a reference to some problems with this approach to the Dirichlet-Miltonomial. I would highly recommend checking Bioconductor or that package documentation because those pseudocounts can easily be just a simple method to convert different matrices while integrating very different distributions.
- Now we estimate the parameters In Dirichlet-multinomial model and update them: $\alpha_1+n_1,\dots,\alpha_k+n_k$ eventually obtaining the posterior distributions and estimating the number of types of linked SNPs that fall into my novel sub-sub-clade with their probabilities to conclude how likely we are to see those groups in the sub-sub-clade.
P.S. I suspect the reason Dirichlet and Multinomial are so applicable to genomics and are used in some Bioinformatics packages in R is probably due to a lot of discretization in these types of dataset and also, traditional models such as the ones based on the Hardy-Weinberg Principle as they are mathematically a perfect candidate of some Binomial, Beta, Multinomial etc type of a setup because you are essentially estimating the frequencies of some counts in some discrete categories (although the Dirichlet does not require the parameters $\alpha$ to be integers.
P.P.S. From a very reduced set up above, I have omitted other important things to consider which can be found in this tutorial, such as Dirichlet Process and specifically, the partition step of some probability space $\Theta$ to find
$$\theta_k | \text{Prior distribution H over component parameters, } \theta_k \sim H$$
