From the dunn.test manual: "CDF of one group does not cross the CDF of the other". What this means? I am not a statistician, but I want to understand. What I found using a Google search not helped me very much :(.
- 165
- 1
- 6
-
@whuber Thank you, but I do not see any duplication, maybe only a partial one. We asked two different things! Anyway, I don't see there an answer to my question. – Iurie Dec 19 '14 at 18:47
-
I checked again. Glen_b's answer points out that "The step-functions can coincide, but the x-sample ecdf will never be above/left of the y-sample ecdf." That is a clear, straightforward (and graphically illustrated) response that directly answers your question. – whuber Dec 19 '14 at 18:59
-
OK! I had to write in bold: I'm not a statistician! :-) For me that was not clear, not understandable, but after the @tim answer now is clear! – Iurie Dec 19 '14 at 19:20
2 Answers
CDF's are Cumulative Distribution Functions, i.e. they tell you about the probability that some value $X$ is less or equal then $x$, $F(x) = P(X \leq x)$.
Below you can see the example of crossing and non crossing CDF's:
set.seed(123)
n <- 1e3
x <- sort(rnorm(n, 0, 1))
y <- sort(rnorm(n, 1, 1))
z <- sort(rnorm(n, .5, 2))
plot(x, (1:n)/n, type="l", xlim=c(-4, 4), ylab="F(x)")
lines(y, (1:n)/n, col="red")
lines(z, (1:n)/n, col="green")
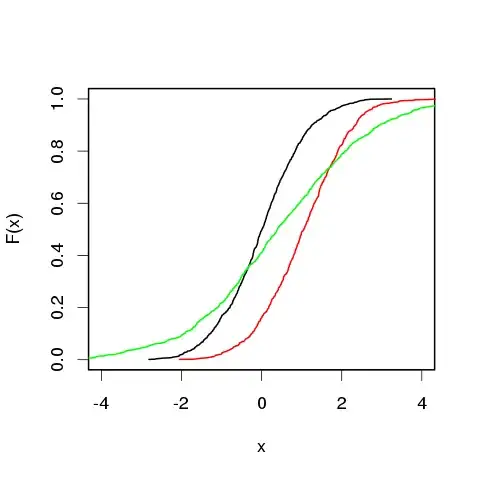
On the y-axis there are cumulative probabilities and on the x-axis values of the variables. Lines black (x) and red (y) do not cross, while green (z) crosses both black and white. What this plot tells you is that values of x and y go in parallel, because the only difference between them is that their mean value is different. Distribution of z is different because it has different standard deviation, so its CDF also differs.
Now, if you read again the manual of dunn.test function in R (bold font by myself):
The interpretation of stochastic dominance requires an assumption that the CDF of one group does not cross the CDF of the other. (...) The null hypothesis for each pairwise comparison is that the probability of observing a randomly selected value from the first group that is larger than a randomly selected value from the second group equals one half; this null hypothesis corresponds to that of the Wilcoxon-Mann-Whitney rank-sum test. Like the rank-sum test, if the data can be assumed to be continuous, and the distributions are assumed identical except for a difference in location, Dunn’s test may be understood as a test for median difference
...you can see the assumption of Dunn test is that the distributions are the same and differ just by location (i.e. mean). This is exactly what is illustrated on the plot I pasted, where x and y have different mean but z has also different standard deviation and so its distribution has different shape.
-
1One minor quibble: the assumption in the discussion of stochastic dominance in relation to Dunn's test is about population distributions, while your illustration is about sample (i.e. empirical) CDFs. – Glen_b Dec 19 '14 at 15:24
-
OK, but I would say that population distribution makes not a very clear example ;) – Tim Dec 19 '14 at 16:40
-
-
Tim -- The example is fine, as is the reference to it for motivation/clarification when discussing the paragraph from the manual; I just thought it important to point out the distinction between the sample and the population -- thinking hypotheses are statements about samples is a common confusion many people carry in respect of hypothesis tests. I believe it pays to emphasize that they are statements about populations when there's any potential for confusion. – Glen_b Dec 19 '14 at 23:16
CDF is a monotonously increasing curve with y-values going from 0 to 1 and x values going through the entire domain. If you draw two curves on the same graph, they may or may not cross each other. They'll definite connect at y=0 and 1.
- 55,939
- 5
- 90
- 176