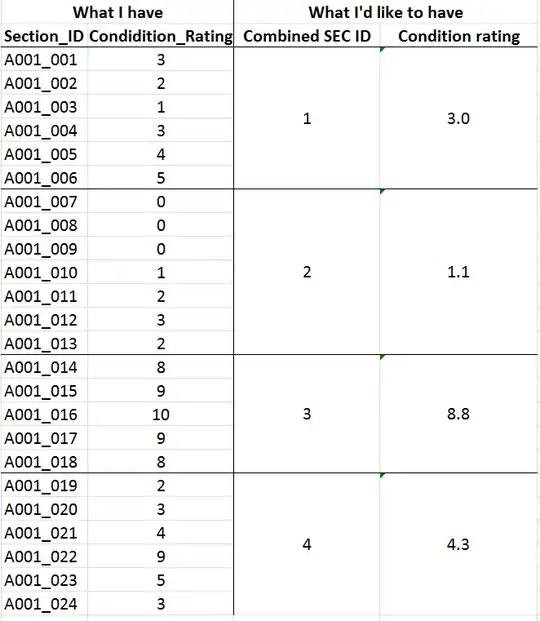
A dynamic program to minimize the sum of group variances subject to these constraints is simple and reasonably fast, especially for such a narrow range of group sizes. It reproduces the posted solution.
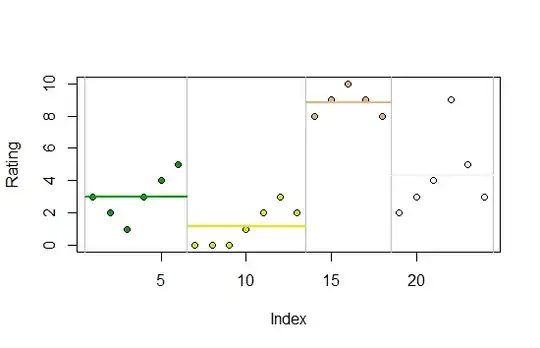
The data are plotted as point symbols. The groups are color-coded and separated by vertical lines. Group means are plotted as horizontal lines.
Commented R code follows. It computes the solution recursively, achieving efficiency by caching the results as it goes along. The program cluster(x,i) finds (and records) the best solution starting at index i in the data array x by searching among all feasible windows of lengths n.min through n.max beginning at index i. It returns the best value found so far (and, within the global variable cache$Breaks, leaves behind an indicator of the indexes that start each group). It can process arrays of thousands of elements in seconds, depending on how large the range n.max-n.min is. For larger problems it would have to be improved to include some branch-and-bound heuristics to limit the amount of searching.
#
# Univariate minimum-variance clustering with constraints.
# Requires a global data structure `cache`.
#
cluster <- function(x, i) {
#
# Cluster x[i:length(x)] recursively.
# Begin with the terminal cases.
#
if (i > cache$Length) return(0) # Nothing to process $
cache$Breaks[i] <<- FALSE # Unmark this break $
if (i + cache$n.min - 1 > cache$Length) return(Inf)# Interval is too short
if (!is.na(v <- cache$Cache[i])) return(v) # Use the cached value $
n.min <- cache$n.min + i-1 # Start of search $
n.max <- min(cache$n.max + i-1, cache$Length) # End of search
if (n.max < n.min) return(0) # Prevents `R` errors
#
# The recursion: accumulate the best total within-group variances.
# To implement other objective functions, replace `var` by any measure of
# within-group homogeneity.
#
values <- sapply(n.min:n.max, function(k) var(x[i:k]) + cluster(x, k+1))
#
# Find and store the best result.
#
j <- which.min(values)
cache$Breaks[n.min + j] <<- TRUE # Mark this as a good break $
cache$Cache[i] <<- values[j] # Cache the result $
return(values[j]) # Pass it to the caller
}
#
# The data.
#
x <- c(3,2,1,3,4,5,0,0,0,1,2,3,2,8,9,10,9,8,2,3,4,9,5,3)
#
# Initialize `cache` to specify the constraints; and run the clustering.
#
system.time({
n <- length(x)
cache <- list(n.min=4, n.max=10, # The length constraints
Cache=rep(NA, n), # Values already found
Breaks=rep(FALSE, n+1), # Group start indexes
Length=n) # Cache size
cluster(x, 1) # I.e., process x[1:n]
cache$Breaks[1] <- TRUE # Indicate the start of the first group $
})
#
# Display the results.
#
breaks <- (1:(n+1))[cache$Breaks] # Group start indexes $
groups <- cumsum(cache$Breaks[-(n+1)]) # Group identifiers
averages <- tapply(x, groups, mean) # Group summaries
colors <- terrain.colors(max(groups)) # Group plotting colors
plot(x, pch=21, bg=colors[groups], ylab="Rating")
abline(v = breaks-1/2, col="Gray")
invisible(mapply(function(left, right, height, color) {
lines(c(left, right)-1/2, c(height, height), col=color, lwd=2)
}, breaks[-length(breaks)], breaks[-1], averages, colors))