@ocram's approach will certainly work. In terms of the dependence properties it's somewhat restrictive though.
Another method is to use a copula to derive a joint distribution. You can specify marginal distributions for success and age (if you have existing data this is especially simple) and a copula family. Varying the parameters of the copula will yield different degrees of dependence, and different copula families will give you various dependence relationships (e.g. strong upper tail dependence).
A recent overview of doing this in R via the copula package is available here. See also the discussion in that paper for additional packages.
You don't necessarily need an entire package though; here's a simple example using a Gaussian copula, marginal success probability 0.6, and gamma distributed ages. Vary r to control the dependence.
r = 0.8 # correlation coefficient
sigma = matrix(c(1,r,r,1), ncol=2)
s = chol(sigma)
n = 10000
z = s%*%matrix(rnorm(n*2), nrow=2)
u = pnorm(z)
age = qgamma(u[1,], 15, 0.5)
age_bracket = cut(age, breaks = seq(0,max(age), by=5))
success = u[2,]>0.4
round(prop.table(table(age_bracket, success)),2)
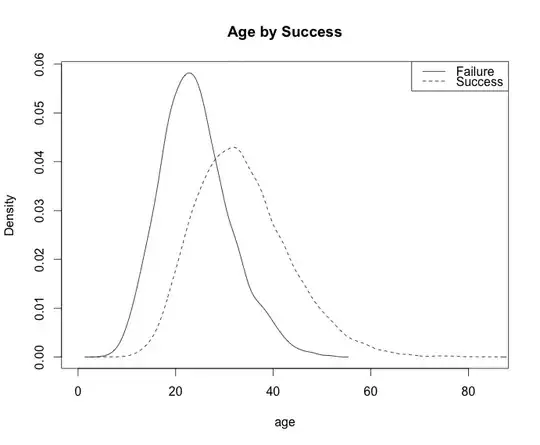
plot(density(age[!success]), main="Age by Success", xlab="age")
lines(density(age[success]), lty=2)
legend('topright', c("Failure", "Success"), lty=c(1,2))
Output:
Table:
success
age_bracket FALSE TRUE
(0,5] 0.00 0.00
(5,10] 0.00 0.00
(10,15] 0.03 0.00
(15,20] 0.07 0.03
(20,25] 0.10 0.09
(25,30] 0.07 0.13
(30,35] 0.04 0.14
(35,40] 0.02 0.11
(40,45] 0.01 0.07
(45,50] 0.00 0.04
(50,55] 0.00 0.02
(55,60] 0.00 0.01
(60,65] 0.00 0.00
(65,70] 0.00 0.00
(70,75] 0.00 0.00
(75,80] 0.00 0.00