2

I am trying to apply some data analysis on data which is generated by picking points from a sine wave with some noise added in. I am purposefully ignoring the time dependence, so just collecting data points and plotting in a histogram you get something like

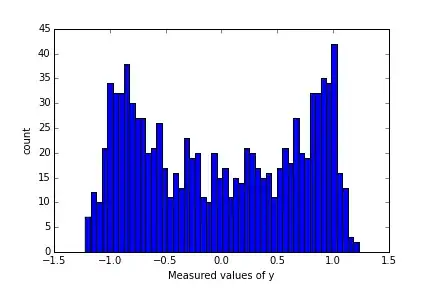
enter image description here

Image generated by (if that helps)

import matplotlib.pyplot as plt
import numpy as np
import pymc as pm

N = 10000
x = np.linspace(0, 2*np.pi, N)
y = np.sin(x) + np.random.normal(0, 0.1, N)
data = y[np.random.randint(0, N, 1000)]

out = plt.hist(data, bins=50)
plt.ylabel("count")
plt.xlabel("Measured values of y")
plt.show()

Now I need to generate a probability model. My current idea is that the measured y will follow a normal distribution with a distribution for its mean. The distribution for its mean should come from picking points from a sine wave without noise.

I know the pdf for picking points from a sine wave without noise, it is given by

P(y) = 1/sqrt(1 - ((y-y0)/A)^2)

where y0 and A are define in the following way: y = y0 + A*sin(t). For more about this, I already asked a question and was kindly helped on this site

So I naively tried to set this as the mean by doing something like (note I am using the data generated above to test my code works)

A = pm.Uniform("A", 0.1, 2)
y0 = pm.Uniform("y0", -10, 10)
std_dev = pm.Uniform('std_dev', lower=0, upper=50)

@pm.deterministic(plot=False)
def precision(std_dev=std_dev):
    return 1.0 / (std_dev * std_dev)

@pm.deterministic
def mean(value=0.1, A=A, y0=y0):
    return 1.0 / np.sqrt(1 - ((value-y0)/A)**2)

observed = pm.Normal("observed", mu=mean, tau=precision, value=data, observed=True)

model = pm.MCMC([observed, std_dev, y0, A])

However the samples don't seem to converge and even stranger I get values of y0 and A outside of the allowed regions.

As you may have guessed I'm fairly new to this. Some background in case it helps: I am attempting to do a model comparison between data generated by a sine wave (as above) and data generated by a square wave which was answered very nicely in this post. Both produce a bimodal distribution so are feasible for the data set.

All advice will be hugely appreciated.

Community
  • 1
Greg
  • 464
  • 3
  • 9

1 Answers1

2

This mostly makes sense. However, since you are computing the means in a deterministic way, you don't need a PDF for that. So replacing the means deterministic formula with y = y0 + A*sin(t) should make this correct.

Hopefully that already will give you the correct answer. Moreover, for circular distributions like that you might also want to look into the von Mises distribution which will probably be a better prior for the phase.

As an aside, you can just set: tau=std_dev**-2 in your likelihood to achieve the same result.

twiecki
  • 1,036
  • 6
  • 5
  • I was trying to avoid using the time dependence, but your suggestion does solve the issue so thanks. One question though, how would you then go about reproducing simulated results given that the mean depends on the data? Or should I ask this as a new question.. – Greg Dec 11 '14 at 14:48
  • 1
    A posterior predictive? I would subsample from the posterior traces and for each sampled parameter set run your data generation procedure from above. – twiecki Dec 12 '14 at 20:01