I want to understand how two quantities X and Z impact Y.
Should I use a single multiple regression model containing the effects of X and Z on Y rather than separate regression models looking at the effects of X on Y and Z on Y?
I think the multiple regression is better but I can't explain why (except reduced error). If not, why?
This is a somewhat confusing debate because I am not sure how the two-regression method is going to achieve your goal.
Regression models with two continuous independent variables can be visualized as a 3-D space:
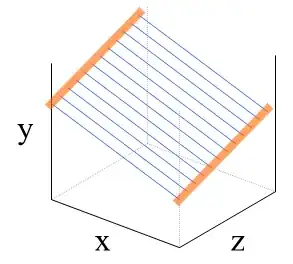
The blue lines represent the association between $x$ and $y$ at each value of $z$. Without $z$ in the model, the slope of the blue line may no longer be the same as the picture above because somehow $z$ could be associated with $x$ and in the same time a causal component of $y$. In such case, missing $z$ in the model will confound the association between $x$ and $y$. Aka, $\beta_1$, the regression coefficient of $x$ in $y = \beta_0 + \beta_1 x$ can be biased.
This 3-variable dynamics cannot be discerned just by examining $x$ on $y$ and $z$ on $y$ separately. I may consider them as an intermediate approach to understand the relationship between variables... but they cannot complete the job if seeing "amount of X given and amount of Z taken impacts Y" is your goal.
To complicate the answer slightly, your proposed method of performing a multiple linear regression with both $x$ and $z$ as independent variables may also be insufficient. Sometimes, the association of an independent variable may depend on the value of another independent variable, causing the regression plane to "warp." This is one of the many possibilities:
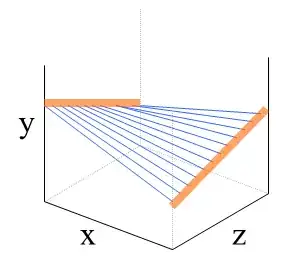
In this case, the association between $x$ and $y$ (the slopes of the blue line) changes at different value of $z$. If this is happening, you may need to modify your model by incorporating an interaction term between $x$ and $z$.
There is also collinearity that can affect the results of your multiple regression model as well.
One way of thinking about why least squares regression (and other methods, but I'm assuming this is what you're asking about) is useful is thinking about the problem of distinguishing different effects. In other words, regression allows us to determine the unique effect that X has on Y and the unique effect that Z has on Y. If X and Z are related together statistically, then simply regressing Y on X will give an erroneous estimate of the effect of X on Y because some of the effect of Z will be caught up in the regression. The same thing happens if you only regress Y on Z. The cool thing about regression is that it allows us to see the unique effect that each predictor has on the response variable, even if our predictors are themselves related.
That being said, it looks like you need to read up or review the basics of regression itself. This is especially true if you're using regression methods to make arguments in a thesis.
This answer to another question, along with the other discussion, may help your understanding.
A big part of it is that x and z may be correlated with each other and you need to take that relationship into account to fully understand how they relate to y. Even if x and z are perfectly orthogonal, accounting for the variance explained by z when looking at the relationship between x and y can reduce the variation and give more precise estimates.
That said, sometimes there are advantages to looking at the individual relationships as well as the multiple regression. You need to think about what question(s) you are trying to answer and what models would answer them.
