I'm learning HMM now and very confused about the order of the Markov chain. Can anybody help me by answering the following question as an example: Thank you very much!
Take 100,000 bases from chromosomes 1 and 2 respectively, what is the transition matrices for first order Markov chain, second order Markov chain, and third order Markov chain. How to draw state diagram for first order Markov chain?
The order of a Markov chain is how far back in the history the transition probability distribution is allowed to depend on.
For a first-order Markov chain, the probability distribution of the next state can only depend on the current state. So your transition matrix will be 4x4, like so:
$$\left(\begin{array}{cccc} P(A \to A) & P(A \to C) & P(A \to T) & P(A \to G) \\ P(C \to A) & P(C \to C) & P(C \to T) & P(C \to G) \\ P(T \to A) & P(T \to C) & P(T \to T) & P(T \to G) \\ P(G \to A) & P(G \to C) & P(G \to T) & P(G \to G) \\ \end{array}\right)$$
(where $P(A \to C)$ is the probability of seeing a $C$ if you just read an $A$, etc.
Now, if you go up to order 2, the probability distribution of the next state can depend on the previous two states. So instead of just looking at $P(A \to C)$, we now need to look at $P(AA \to C), P(CA \to C), P(TA \to C), P(GA \to C)$. This will result in a $16 \times 16$ transition matrix that I don't really want to write out, but hopefully you get the idea.
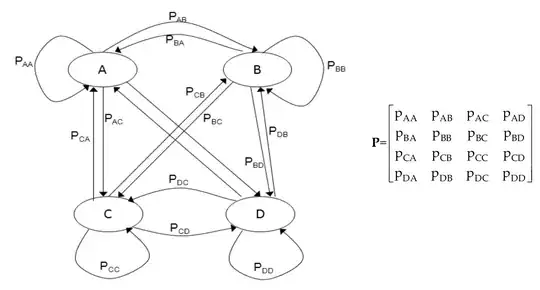
As for drawing the state diagram, you can find some examples online--the basic idea is that you draw a circle for each state, an arrow between each two states with transitions, and label each arrow with the transition probability. Here's an example with four states (from here):
