Kurtosis is certainly not the location of where the peak is. As you say, that's already called the mode.
Kurtosis is the standardized fourth moment: If $Z=\frac{X-\mu}{\sigma}$, is a standardized version of the variable we're looking at, then the population kurtosis is the average fourth power of that standardized variable; $E(Z^4)$. The sample kurtosis is correspondingly related to the mean fourth power of a standardized set of sample values (in some cases it is scaled by a factor that goes to 1 in large samples).
As you note, this fourth standardized moment is 3 in the case of a normal random variable. As Alecos notes in comments, some people define kurtosis as $E(Z^4)-3$; that's sometimes called excess kurtosis (it's also the fourth cumulant). When seeing the word 'kurtosis' you need to keep in mind this possibility that different people use the same word to refer to two different (but closely related) quantities.
Kurtosis is usually either described as peakedness* (say, how sharply curved the peak is - which was presumably the intent of choosing the word "kurtosis") or heavy-tailedness (often what people are interested in using it to measure), but in actual fact the usual fourth standardized moment doesn't quite measure either of those things.
Indeed, the first volume of Kendall and Stuart give counterexamples that show that higher kurtosis is not necessarily associated with either higher peak (in a standardized variable) or fatter tails (in rather similar way that the third moment doesn't quite measure what many people think it does).
However in many situations there's some tendency to be associated with both, in that greater peakedness and heavy tailedness often tend to be seen when kurtosis is higher -- we should simply beware thinking it is necessarily the case.
Kurtosis and skewness are strongly related (the kurtosis must be at least 1 more than the square of the skewness; interpretation of kurtosis is somewhat easier when the distribution is nearly symmetric.
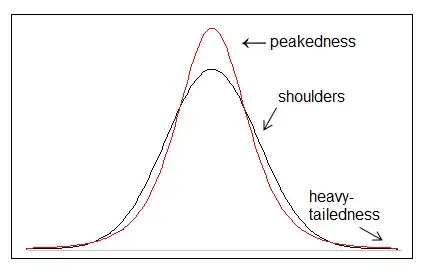
Darlington (1970) and Moors (1986) showed that the fourth moment measure of kurtosis is in effect variability about "the shoulders" - $\mu\pm\sigma$, and Balanda and MacGillivray (1988) suggest thinking of it in vague terms related to that sense (and consider some other ways to measure it). If the distribution is closely concentrated about $\mu\pm\sigma$, then kurtosis is (necessarily) small, while if the distribution is spread out away from $\mu\pm\sigma$ (which will tend to simultaneously pile it up in the center and move probability into the tails in order to move it away from the shoulders), fourth-moment kurtosis will be large.
De Carlo (1997) is a reasonable starting place (after more basic resources like Wikipedia) for reading about kurtosis.
Edit: I see some occasional questioning of whether higher peakedness (values near 0) can affect kurtosis at all. The answer is yes, definitely it can. That this is the case is a consequence of it being the fourth moment of a standardized variable -- to increase the fourth moment of a standardized variate you must increase $E(Z^4)$ while holding $E(Z^2)$ constant. This means that movement of probability further into the tail must be accompanied by some further in (inside $(-1,1)$); and vice versa -- if you put more weight at the center while holding the variance at 1, you also put some out in the tail.
[NB as discussed in comments this is incorrect as a general statement; a somewhat different statement is required here.]
This effect of variance being held constant is directly connected to the discussion of kurtosis as "variation about the shoulders" in Darlington and Moors' papers. That result is not some handwavy-notion, but a plain mathematical equivalence - one cannot hold it to be otherwise without misrepresenting kurtosis.
Now it's possible to increase the probability inside $(-1,1)$ without lifting the peak. Equally, it's possible to increase the probability outside $(-1,1)$ without necessarily making the distant tail heavier (by some typical tail-index, say). That is, it's quite possible to raise kurtosis while making the tail lighter (e.g. having a lighter tail beyond 2sds either side of the mean, say).
[My inclusion of Kendall and Stuart in the references is because their discussion of kurtosis also relevant to this point.]
So what can we say? Kurtosis is often associated with a higher peak and with a heavier tail, without having to occur wither either. Certainly it's easier to lift kurtosis by playing with the tail (since it's possible to get more than 1 sd away) then adjusting the center to keep variance constant, but that doesn't mean that the peak has no impact; it assuredly does, and one can manipulate kurtosis by focusing on it instead. Kurtosis is largely but not only associated with tail heaviness -- again, look to the variation about the shoulders result; if anything that's what kurtosis is looking at, in an unavoidable mathematical sense.
References
Balanda, K.P. and MacGillivray, H.L. (1988),
"Kurtosis: A critical review."
American Statistician 42, 111-119.
Darlington, Richard B. (1970),
"Is Kurtosis Really "Peakedness?"."
American Statistician 24, 19-22.
Moors, J.J.A. (1986),
"The meaning of kurtosis: Darlington reexamined."
American Statistician 40, 283-284.
DeCarlo, L.T. (1997),
"On the meaning and use of kurtosis."
Psychol. Methods, 2, 292-307.
Kendall, M. G., and A. Stuart,
The Advanced Theory of Statistics,
Vol. 1, 3rd Ed.
(more recent editions have Stuart and Ord)
