cost function in logistic regression vs optimization algorithms

Question

I have a table like:

    tabla <-data.frame(c=c(-3, -2, -1, -1, 1, 2, 3, 0, 0, 5, 4, 
              3,  0, 8, 9, 10, 6, 6, 7, 3, 0), e=c(0, 0, 0, 0, 0, 
              0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 0, 1, 1, 0, 1))
    tabla <- tabla[order(tabla$c), ]

Let's suppose I need to predict e with c using a logistic regression:

    log_pru <- glm(e ~ c, data = tabla, family = binomial(logit))
    tabla$pred_res <- predict(log_pru, tabla, type = "response")

Let's suppose also that my gain is 90 when my choice is TP, and -10 when is FP function is:

    mycost <- function(r, pi){
      weightTP = -90 #cost for getting 1 ok -90
      weightFP = 10 #cost for getting 0 wrong 10
      cTP = (r==1)&(pi==1) #logical vector--- true is actual==1 
                           #and predict ==1
      cFP = (r==0)&(pi==1) #logical vector - true if actual 0 
                           #but predict 1
      return(mean(weightTP*cTP+weightFP*cFP))
    }

If I'm able to identify each TP without FP, my gain would be:

    maxgain <- tabla$e*90
    sum(maxgain)
     630

In the log model, my gain would be:

    tabla$ganLog <- ifelse(tabla$pred_res>.1, tabla$e*90-10, 0)

which is 420.

I thought that introducing the cost function in the optimizing algorithm might be useful to reflect my actual problem.

So, to use "optim", I wrote the following function (which is a sigmoidal):

    fn <- function(x) { 
      alpha <- x[1]
      beta <- x[2] 
      J <- exp(alpha + tabla$c * beta)
  prediction <- ifelse(J/(1+J) > 0.5, 1, 0)
  mycost(tabla$e, prediction)  
    }

    guess <- optim(c(0,0), fn, method='SANN')

And my result is:

    alpha <- guess$par[1]
beta <- guess$par[2]
    J<-exp(alpha + tabla$c * beta)
tabla$pred_guess = J/(1+ J)
    plot(tabla$c, tabla$e)
    lines(tabla$c, tabla$pred_guess)
    mycost(tabla$e, ifelse(tabla$pred_res > 0.1, 1, 0))

    tabla$ganOpt<-ifelse(tabla$pred_guess>.5, tabla$e*90-10,0)
sum(tabla$ganOpt)

Which is 460. (almost 10% greater than the obtained by the logistic with glm). If I plot both graphs:

    plot(e ~ c, data=tabla)
    lines(tabla$c, log_pru$fitted, type="l", col="red")
    abline(0.1, 0)
    abline(v=min(tabla$c[tabla$pred_res>0.1]), col="blue")

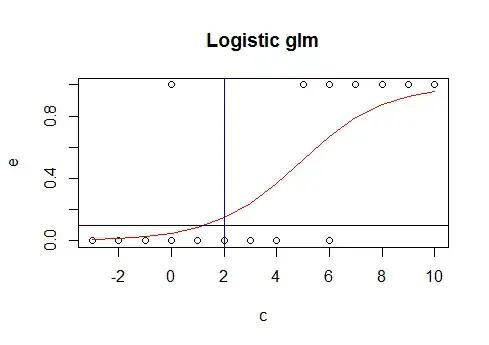
Logistic model and threshold selection >.1

An the other model would be:

    plot(tabla$c, tabla$e, main="optim")
    lines(tabla$c, tabla$pred_guess, col="red")
    abline(0.5, 0)
    abline(v=min(tabla$c[tabla$pred_guess>0.5]), col="blue")

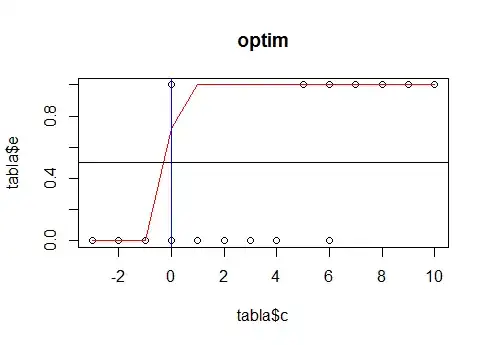
optim model and threshold selection

I know that you can introduce a cost function in cv.glm but this is only o select among models already chosen, so, my questions are:

Would it be a good idea to introduce a cost function in the algorithm that selects the parameters?
What does SAS do with the cost function in Miner? Does it use it to select the parameters values?
Why glm package in R doesn't have the possibility to introduce another cost function?
Would it be a bad idea to use "optim" in real examples? What about over-fitting? And also, do I have to program all the variables like I did in this mini example? Is there a better way?
What about doing oversampling or downsampling to avoid this?

I would really appreciate a theoretical answer.

score 7 · Accepted Answer · answered Nov 29 '14 at 13:05

7

If I understand what you have done, you have done things out of order. Maximum likelihood or penalized maximum likelihood estimation is the gold standard method for estimating parameters in a regression model. The cost function does not apply to how one estimates risk. The cost function is applied to individual risk estimates to provide an optimum decision for that one observation.

answered Nov 29 '14 at 13:05

Frank Harrell

74,029
5
148
322

thanks Frank. I understand but in this case I'm loosing the opportunity to gain because I'm not introducing the cost function in the method for estimating parameters....Why? and ...What do you think would be better in this way? – GabyLP Nov 29 '14 at 13:17
3

The cost/loss/utility function is applied to individual optimum predictions to obtain optimal decisions. Here is an analogy: Suppose you want to make the best medical decision about a disease a patient may have. You get an estimate of the probability that the patient has the disease irrespective of the cost function that may apply to later decisions. Now the physician discusses this with the patient and finds the patient has a certain cost function that was not expected. An optimum treatment is selected for that patient. The cost function depended on initially unavailable variables. – Frank Harrell Nov 29 '14 at 13:37
@FrankHarrell What would you, then, think of [this](https://stats.stackexchange.com/a/538524/247274) example, where it seems like we profit the most by building our model based on classification accuracy, rather than accuracy of probability predictions? – Dave Dec 09 '21 at 16:18
I wish I had time to understand that long example. In general it's impossible for classification accuracy to have anything to do with optimum decisions. Perhaps there is a discontinuous degenerate case where my statement doesn't hold. – Frank Harrell Dec 09 '21 at 16:21

cost function in logistic regression vs optimization algorithms

1 Answers1